2022 LGS Matematik Çıkmış Sorular

a ≠ 0, b ≠ 0 ve k, m, n tam sayılar olmak üzere

(aⁿ)ᵐ ve (a.b)ᵏ = aᵏ . bᵏ dir.

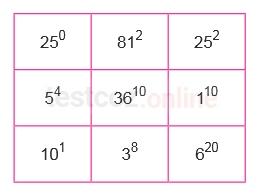
Yukarıda verilen dokuz adet kutudan her birine bir üslü ifade yazılmıştır. Bu üslü ifadelerden birbirine denk olanların bulunduğu kutular aynı renge boyanacaktır.

Buna göre, boyanmayan kutudaki üslü ifade aşağıdakilerden hangisidir?

|a|, 1 veya 1’den büyük, 10’dan küçük bir gerçek sayı ve n bir tam sayı olmak üzere a . 10ⁿ gösterimi “bilimsel gösterim”dir.

Aşağıdaki tabloda bir bitkinin aylık uzama miktarları verilmiştir.

Tablo: Bitkinin Aylara Göre Uzama Miktarı

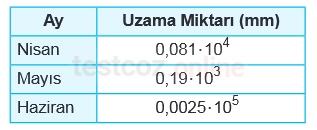
Buna göre, bu bitkinin tablodaki üç aylık toplam uzama miktarının milimetre cinsinden bilimsel gösterimi aşağıdakilerden hangisidir?

a, b, c, d birer doğal sayı olmak üzere

a√b = √a²b

a√b + c√b = (a+c) √b

a√b - c√b = (a-c) √b

a√b . c√d = (a.c) √b.d dir.

Çevresinin uzunluğu √800 cm olan dikdörtgen şeklindeki kâğıt, yukarıdaki gibi dikdörtgen ve kare şeklinde iki parçaya ayrılıyor.

Kare şeklindeki parçanın bir kenarının uzunluğu √8 cm olduğuna göre dikdörtgen şeklindeki parçanın bir yüzünün alanı kaç santimetredir?

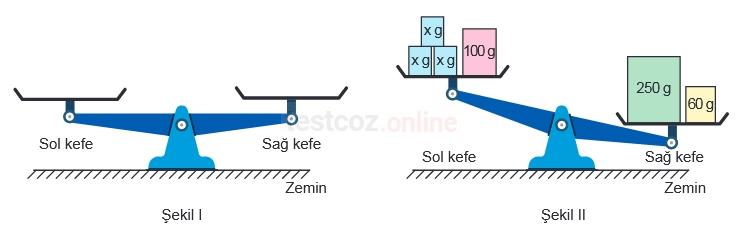
Denge durumundaki eşit kollu terazinin kefelerinin konumu Şekil I’deki gibidir. Bu terazinin sol kefesine bir adet 100 gramlık ve üç adet x gramlık kutu, sağ kefesine ise bir adet 250 gramlık ve bir adet 60 gramlık kutu yerleştirildiğinde denge durumu bozulan terazinin kefelerinin konumu Şekil II’deki gibi olmuştur.

Buna göre, x’in alabileceği değerleri gösteren eşitsizlik aşağıdakilerden hangisidir?

Zeynep’in kalem sayısının çarpanlarından kendisi hariç en büyük iki çarpanı ile Kuzey’in kalem sayısının çarpanlarından kendisi hariç en büyük iki çarpanı aşağıda gösterilmiştir.

Zeynep ve Kuzey, yukarıda verilen çarpanların toplamı kadar kalemi arkadaşlarına vermiştir.

Buna göre, Zeynep ve Kuzey’in toplam kaç kalemi kalmıştır?

Bir fabrikanın üç farklı ürün bandında paketlenen ürün sayıları ve bu ürünlerin paketlenme süreleri aşağıdaki tabloda verilmiştir.

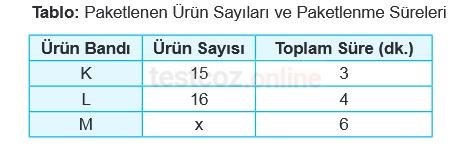
Bu üç bandın her birinde 1 dakikada paketlenen ürün sayısı bir doğal sayıya eşit ve toplamları 13’ten azdır.

Buna göre, x’in alabileceği değer en fazla kaçtır?

Mavi dikdörtgensel bölgenin kısa kenarı 4 cm, uzun kenarı ise 2 cm uzatılarak alanı

(9x²+ 24x + 16) cm² olan aşağıdaki karesel bölge elde edilecektir.

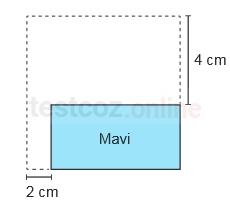
Buna göre, mavi dikdörtgensel bölgenin çevresinin uzunluğunu santimetre cinsinden veren cebirsel ifade aşağıdakilerden hangisidir?

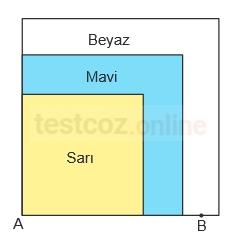
Kare şeklindeki sarı, mavi ve beyaz kartlar, ikişer kenarları ve birer köşeleri A noktasında çakışacak biçimde üst üste yapıştırılarak aşağıdaki şekil elde edilmiştir.

Şekilde görünen farklı renkteki bölgelerin alanları birbirine eşit ve sarı bölgenin çevresinin uzunluğu 20 cm’dir.

A noktasına uzaklığı santimetre cinsinden doğal sayı olacak biçimde, beyaz bölgenin kenarında şekildeki gibi bir B noktası işaretleniyor.

Buna göre, A ve B noktaları arasındaki uzaklık kaç santimetredir?

Bir süt fabrikasında muz aroması ile muzlu süt, çilek aroması ile çilekli süt yapılmaktadır. Elde edilen meyveli sütler özdeş kutulara boşluk kalmayacak biçimde doldurulmaktadır.

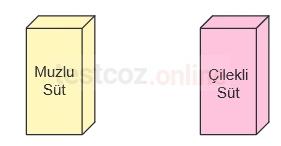
Bir günde üretilen muzlu süt ve çilekli süt miktarı daire grafiğinde ve bu meyveli sütlerde kullanılan aromaların toplam miktarı kareli zeminde verilen sütun grafiğinde aşağıda gösterilmiştir.

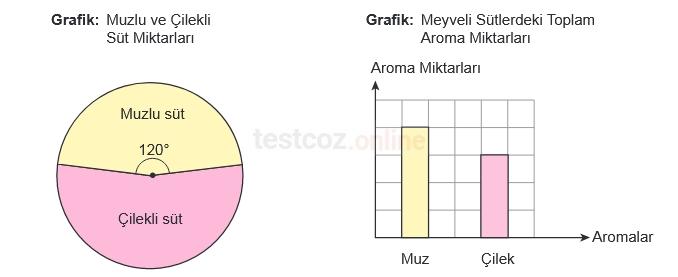
Buna göre, bir kutu muzlu sütteki muz aromasının, bir kutu çilekli sütteki çilek aromasına oranı kaçtır?

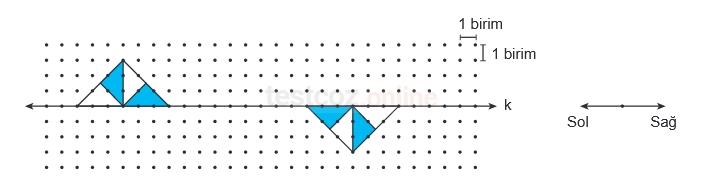
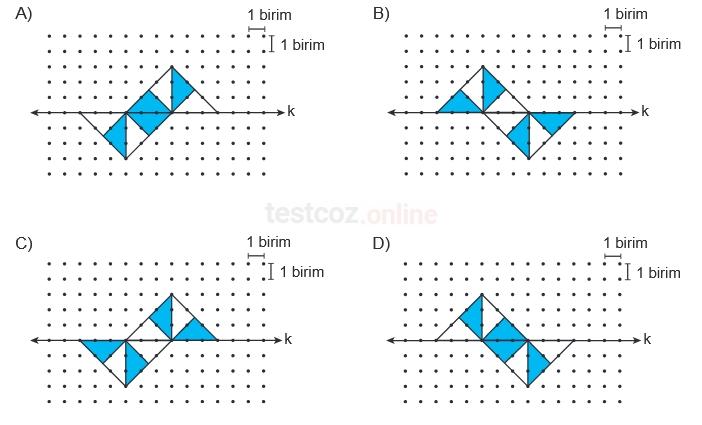
Noktalı kâğıt üzerinde verilen k doğrusu boyunca soldaki şekil 6 birim sağa, sağdaki şekil ise 6 birim sola ötelendikten sonra her ikisinin de k doğrusuna göre yansıma altındaki görüntüleri oluşturuluyor.

Buna göre, oluşan görüntüler aşağıdakilerden hangisidir?

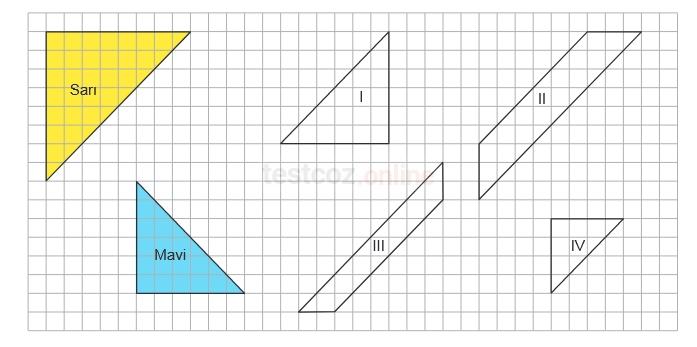
Yukarıdaki kareli zemin üzerinde geometrik şekiller verilmiştir.

Mavi renkli üçgenin bir kenarıyla, numaralanmış şekillerden hangisinin bir kenarı çakıştırıldığında sarı üçgene eş bir üçgen elde edilir?

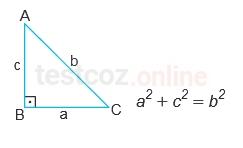
Dik üçgenlerde 90° lik açının karşısındaki kenara “hipotenüs” denir. Bir dik üçgende dik kenarların uzunluklarının kareleri toplamı, hipotenüsün uzunluğunun karesine eşittir.

Kare şeklindeki sarı ve mavi kâğıtlar, birer köşeleri ve birer kenarları Şekil Iʼdeki gibi çakıştırılmıştır.

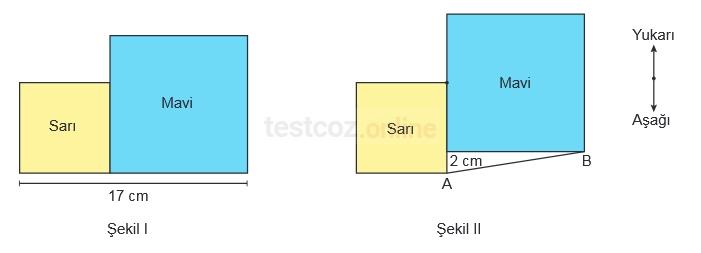
Kâğıtlar Şekil Iʼdeki konumundayken sarı kâğıt sabit kalmak üzere mavi kâğıt yukarı doğru 2 cm hareket ettirildiğinde sarı kâğıdın bir köşesi, mavi kâğıdın kenarının orta noktası ile

Şekil IIʼdeki gibi çakışmıştır.

Buna göre, Şekil IIʼde iki köşeyi birleştiren AB doğru parçasının uzunluğu kaç santimetredir?

Kısa kenarlarının uzunlukları x cm olan dikdörtgen şeklindeki 12 adet kâğıt uzun kenarlarından çakıştırılarak aşağıdaki şekil elde edilmiştir.

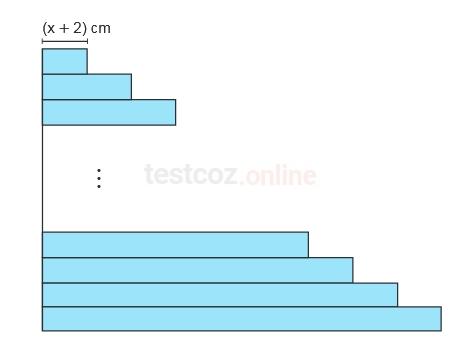
Bu kâğıtlar; en üstteki kâğıdın uzun kenarının uzunluğu (x + 2) cm olmak üzere sonraki her kâğıt, bir önceki kâğıttan 2 cm daha uzun olacak biçimde yerleştirilmiştir.

Buna göre, oluşan şeklin bir yüzünün alanını santimetrekare cinsinden veren cebirsel ifade aşağıdakilerden hangisidir?

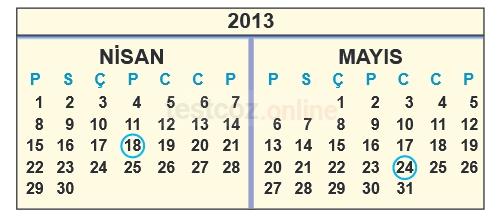
Öğrenci sayısı 20 olan bir sınıftaki her bir öğrencinin doğum tarihi birbirinden farklıdır. Bu sınıfın öğrenci listesi, öğrencilerin doğum tarihlerine göre büyükten küçüğe doğru sıralanarak oluşturulmuştur. Listenin ilk sırasındaki öğrencinin doğum tarihi 18 Nisan 2013, son sırasındaki öğrencinin doğum tarihi 24 Mayıs 2013 olmuştur.

Bu listeden rastgele seçilen bir öğrencinin doğum tarihinin nisan ayında olma olasılığı, mayıs ayında olma olasılığından daha fazladır.

Buna göre, doğum tarihi 25 Nisan 2013’ten önce olan en az kaç öğrenci vardır?

Eğim, dikey uzunluğun yatay uzunluğa oranıdır.

Dikdörtgen şeklindeki bir levha, mavi renkli bir küpün bir ayrıtı ile çakışacak ve eğimi %40 olacak biçimde zemin üzerine aşağıdaki gibi yerleştirilerek bir rampa elde edilmiştir.

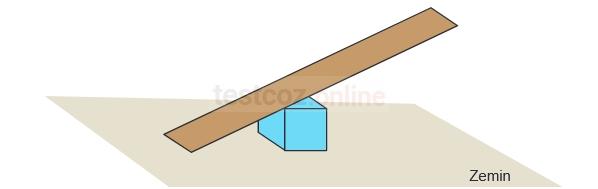
Bu rampanın eğimi değişmeyecek biçimde mavi küp ile özdeş üç sarı küp aşağıdaki gibi taban yüzlerinin tamamı çakışacak biçimde üst üste zemine yerleştirildiğinde, levhanın bir kenarı üstteki sarı küpün bir ayrıtı ile çakışmıştır. Bu durumda mavi küp ile zemine temas eden sarı küp arasındaki uzaklık 200 cm’dir.

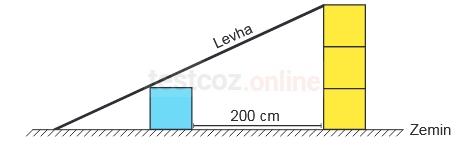
Buna göre, bu küplerden birinin bir ayrıtının uzunluğu kaç santimetredir?

Aşağıda merkezi O noktası olan daire şeklindeki kâğıt, iki eş parçaya bölünerek biri mavi, diğeri sarı renge boyanıyor. Mavi kâğıt, her birinin merkez açısının ölçüsü birbirine eşit olan 12 eş parçaya, sarı kâğıt ise her birinin merkez açısının ölçüsü derece cinsinden doğal sayı olan eş parçalara aşağıdaki gibi bölünüyor.

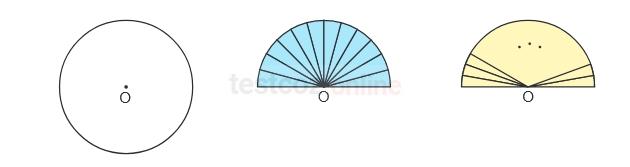
Mavi ve sarı kâğıtların O noktaları bir ABC üçgeninin B ve C köşeleri ile aşağıdaki gibi çakıştırılıyor.

Bu durumda B açısının ölçüsü mavi kâğıdın 5 eş parçasına, C açısının ölçüsü ise sarı kâğıdın 5 eş parçasına eşit olmaktadır.

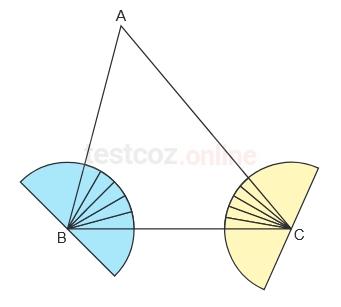
ABC üçgeninde |AC| > |BC| > |AB| olduğuna göre A açısının ölçüsü en az kaç derecedir?

a, b, c birer doğal sayı olmak üzere

a√b = √a²b

a√b + c √b = (a+c) √b

a√b - c √b  = (a-c) √b dir.

Aşağıdaki oyun parkurunda birbirine paralel olan başlangıç çizgisi ve mavi çizgi arasındaki uzaklık 5√3 m’dir. Başlangıç çizgisinden Fatih, Yavuz ve Mehmet doğrusal bir çizgi boyunca top yuvarlayacaklardır. Topu, mavi çizgiye en yakın mesafede duran kişi oyunu kazanacaktır.

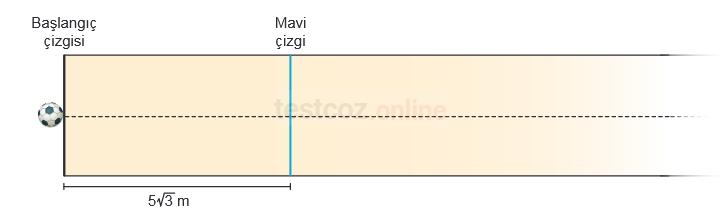
Oyunun sonunda Fatih’in yuvarladığı topun durduğu noktanın mavi çizgiye uzaklığı √3 m, Yavuz’un yuvarladığı topun durduğu noktanın başlangıç çizgisine uzaklığı ise 3√3 m'dir. Bu durumda Fatih birinci, Mehmet ikinci ve Yavuz üçüncü olmuştur.

Buna göre, Mehmet’in yuvarladığı topun durduğu noktanın başlangıç çizgisine uzaklığının metre cinsinden değeri aşağıdakilerden hangisi olabilir?

Bir çiftlikte üretilen süt, cam şişelere ve kâğıt kutulara boşluk kalmayacak biçimde doldurulacaktır.

Bu ürünlerin birer adetlerinin hacimleri ve fiyatları aşağıdaki tabloda verilmiştir.

Tablo: Dolum Yapılacak Ürünlere Ait Bilgiler

Bu çiftlikte üretilen 150 litre sütün tamamını doldurmak için eşit sayıda cam şişe ve kâğıt kutu satın alınıyor. Dolum yapılmadan önce cam şişelerden bir kısmı kırılıyor. Kırılan şişelerin hacmi kadar sütün doldurulabilmesi için kâğıt kutulardan tekrar satın alınıyor.

Bu iş için cam şişelere ve kâğıt kutulara toplam 7400 kuruş ödendiğine göre kırılan cam şişe sayısı kaçtır?

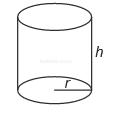
Yarıçapının uzunluğu r, yüksekliği h olan dik dairesel silindirin hacmi πr²h dir.

Yukarıda bir ürüne ait dik dairesel silindir şeklindeki konserve kutusu ve bu kutunun açınımı verilmiş

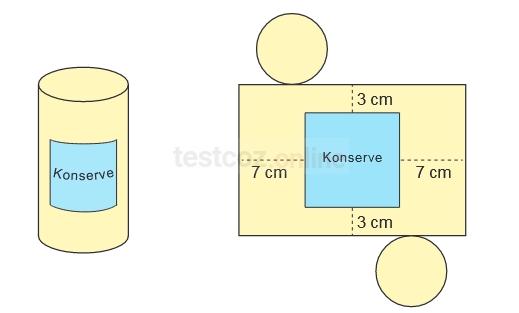
Yukarıda bir ürüne ait dik dairesel silindir şeklindeki konserve kutusu ve bu kutunun açınımı verilmiştir. Bu açınım üzerinde, alanı 100 cm² olan mavi karesel bölgenin kenarları, yanal yüzeyin kenarlarına paraleldir. Mavi bölgenin kenarlara olan uzaklıkları ise şekildeki gibi 3 cm ve 7 cm’dir.

Buna göre, bu konserve kutusunun hacmi kaç santimetreküptür?

(p yerine 3 alınız.)

Aşağıda üzerinde alanları verilen altı adet tarla, hacmi 4000 litre olan tamamı dolu bir depodaki su ile sulanmaktadır.

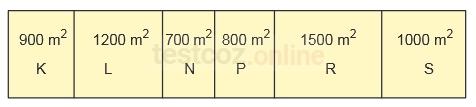
Bu depoda kalan su miktarının ve sulanan alanın zamana göre değişimi aşağıdaki doğrusal grafiklerde gösterilmiştir.

Her bir tarlanın tamamı sulandıktan sonra diğer tarlaya geçilecek şekilde sırasıyla K, L, N, P, R, S tarlaları sulanacaktır.

Buna göre, depoda kalan su miktarının 2500 litrenin altına düştüğü anda hangi tarla sulanmaktadır?