6. Sınıf Matematik Bursluluk Deneme Sınavı
Tebrikler! 6. Sınıf Matematik Bursluluk Deneme Sınavı adlı sınavı başarıyla tamamladınız.
→ Toplam soru sayısı: %%TOTAL%%
→ Doğru sayınız: %%SCORE%% - yanlış ve boş sayınız: %%WRONG_ANSWERS%%.
→ Sınavdan aldığınız başarı yüzdesi: %%PERCENTAGE%%
→ Sınav sonucu değerlendirmeniz: %%RATING%%
Soru 1 |
[36 : 9 + 5 x 8] – [20:5] işleminin sonucu kaçtır?
A | 40 |
B | 36 |
C | 30 |
D | 24 |
TESTCOZ.ONLINE ile başarıya ulaşın!
Bu soruyu adım adım çözerek doğru sonuca ulaşalım:
1. Parantez İçindeki İşlemleri Yapın:
- İlk parantez: \[36 : 9 + 5 \times 8\]
1. 36 : 9 işlemini yapalım. 36'yı 9'a böldüğümüzde 4 elde ederiz.
2. Sıradaki işlem çarpma işlemi olduğu için önce onu yapacağız: 5 \times 8 işlemi 40 eder.
3. Şimdi bu sonuçları toplarız: 4 + 40 = 44
- İkinci parantez: \[20 : 5\]
1. 20'yi 5'e böldüğümüzde 4 elde ederiz.
2. Parantezlerin Sonuçlarını Çıkarın:
- Birinci parantezin sonucu 44, ikinci parantezin sonucu 4.
- Bu iki sonucu birbirinden çıkarırız: 44 - 4 = 40
Sonuç:
Sorunun çözümünde parantez içi işlemleri doğru bir şekilde yaparak ve işlemlerin sırasına dikkat ederek sonuca ulaştık. Doğru Cevap: A) 40
TESTCOZ.ONLINE öğretmeniniz açıklıyor: Bu tür sorularda parantez içi işlemleri öncelikli olarak yapmayı unutmayın. İşlem önceliği kurallarına her zaman dikkat edin: Parantez, çarpma/bölme, toplama/çıkarma sırasını takip edin. Bu kurallar, matematik problemlerini doğru bir şekilde çözmenizi sağlar.
Soru 2 |
97 x… = 0
101 x …. = 101
19 +….. = 35 + 19
13 x (17 + 8 ) = ... x 17 + 13 x 8
Yukarıdaki işlemlerde boş bırakılan yerlere aşağıdaki sayılar yerleştirildiğinde hangi sayı açıkta kalır?
A | 5 |
B | 13 |
C | 35 |
D | 48 |
Bu tür sorular, verilen matematiksel ifadelerdeki boşlukları uygun sayılarla doldurduğumuzda hangi sayının açıkta kalacağını bulmamızı ister. TESTCOZ.ONLINE çözümleri sunar ve bu tür soruları çözmek için adım adım ilerleyeceğiz.
1. Adım: İlk İşlem
- 97 x … = 0 ifadesinde herhangi bir sayı ile çarpıldığında sonuç sıfır oluyorsa, bu sayı sıfırdır. Yani, boşluğa 0 koymalıyız.
2. Adım: İkinci İşlem
- 101 x … = 101 ifadesinde, bir sayı ile çarpıldığında sonuç aynı kalıyorsa, bu sayı 1'dir. Yani, boşluğa 1 koymalıyız.
3. Adım: Üçüncü İşlem
- 19 + … = 35 + 19 ifadesinde, 19'a eklenen sayının 35 ile aynı olması için boşluğa 35 koymalıyız. Çünkü 19 + 35 = 35 + 19 olur.
4. Adım: Dördüncü İşlem
- 13 x (17 + 8 ) = … x 17 + 13 x 8 ifadesi, çarpma işleminin dağılma özelliğini kullanıyor. Bu özellikte, 13 x (17 + 8) = 13 x 17 + 13 x 8 olur. Burada, çarpan 13'tür, yani boşluğa 13 koymalıyız.
Şimdi Yerleştirdiğimiz Sayıları Gözden Geçirelim:
- 0 (97 x 0 = 0)
- 1 (101 x 1 = 101)
- 35 (19 + 35 = 35 + 19)
- 13 (13 x (17 + 8) = 13 x 17 + 13 x 8)
Sonuç:
- Kullanılan sayılar: 0, 1, 35, 13
- Açıkta kalan sayı: A) 5
Doğru Cevap: A) 5
Bu tür soruların çözümünde, verilen ifadelerle matematiksel operasyonların temel özelliklerini kullanmak önemlidir. TESTCOZ.ONLINE ile başarıya ulaşın! 😊
Soru 3 |
Aşağıdaki sayılardan hangisi hem 4 hem de 9 ile tam bölünebilir?
A | 1800 |
B | 1906 |
C | 2709 |
D | 2800 |
TESTCOZ.ONLINE çözümleri sunar 🌟
Bu soruda, verilen sayılardan hangisinin hem 4 hem de 9 ile tam bölünebildiğini bulmamız isteniyor. Şimdi adım adım çözümleyelim:
1. 4 ile Bölünebilme Kuralı:
- Bir sayının 4 ile tam bölünebilmesi için son iki basamağının oluşturduğu sayının 4 ile tam bölünmesi gerekir.
2. 9 ile Bölünebilme Kuralı:
- Bir sayının 9 ile tam bölünebilmesi için rakamlarının toplamının 9 ile tam bölünmesi gerekir.
Şimdi seçenekleri inceleyelim:
A) 1800:
- 4 ile bölünebilme: Son iki basamak "00". 00, 4 ile tam bölünür. ✅
- 9 ile bölünebilme: 1 + 8 + 0 + 0 = 9. 9, 9 ile tam bölünür. ✅
B) 1906:
- 4 ile bölünebilme: Son iki basamak "06". 06, 4 ile tam bölünmez. ❌
- 9 ile bölünebilme: 1 + 9 + 0 + 6 = 16. 16, 9 ile tam bölünmez. ❌
C) 2709:
- 4 ile bölünebilme: Son iki basamak "09". 09, 4 ile tam bölünmez. ❌
- 9 ile bölünebilme: 2 + 7 + 0 + 9 = 18. 18, 9 ile tam bölünür. ✅
D) 2800:
- 4 ile bölünebilme: Son iki basamak "00". 00, 4 ile tam bölünür. ✅
- 9 ile bölünebilme: 2 + 8 + 0 + 0 = 10. 10, 9 ile tam bölünmez. ❌
Sonuç:
Yukarıdaki analizlere göre, sadece 1800 hem 4 hem de 9 ile tam bölünebiliyor. Bu nedenle doğru cevap A) 1800.
Doğru Cevap: A 🎉
TESTCOZ.ONLINE öğretmeniniz açıklıyor: Bu tür sorularda dikkat etmemiz gereken şey, her iki bölünebilme kuralını da ayrı ayrı kontrol etmektir. Böylece doğru sonuca rahatlıkla ulaşabiliriz! 🌟
Soru 4 |
15 sayısının çarpanları olan iki doğal sayının toplamları en çok kaçtır?
A | 8 |
B | 10 |
C | 16 |
D | 20 |
Çözüm:
1. 15 sayısının çarpanlarını bulalım.
- 15 sayısının çarpanları, 1, 3, 5 ve 15'tir. Çünkü bu sayılar 15'i kalansız böler.
2. Çarpan çiftlerini belirleyelim.
- 1 ve 15
- 3 ve 5
3. Her çiftin toplamını hesaplayalım.
- 1 ve 15: 1 + 15 = 16
- 3 ve 5: 3 + 5 = 8
4. Toplamları karşılaştıralım.
- 1 + 15 = 16 ✅
- 3 + 5 = 8
5. En yüksek toplamı belirleyelim.
- 1 ve 15 çiftinin toplamı olan 16, en yüksek toplamdır.
Sonuç:
15 sayısının çarpanlarından oluşan çiftlerin toplamları arasında en yüksek olan 16 değeridir. Bu nedenle doğru cevap C seçeneğidir.
Doğru Cevap: C) 16
TESTCOZ.ONLINE çözümleri sunar ve bu tür sorularla başarıya ulaşmanız daha kolay olur. Keep practicing! 🌟
Soru 5 |
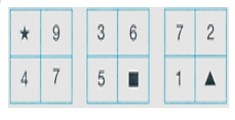
Yukarıdaki kutuların içinde bulunan sayıların her birinin toplamı eşit ve 23’tür.
Buna göre, ![]() toplamının değeri kaçtır?
toplamının değeri kaçtır?
A | 25 |
B | 26 |
C | 27 |
D | 28 |
Bu soruyu adım adım çözerek doğru cevabı bulalım.
1. Adım: İlk Kutunun Toplamı
- İlk kutuda yer alan sayılar: \( \star, 9, 4, 7 \)
- Toplamları 23 olduğuna göre:
\[
\star + 9 + 4 + 7 = 23
\]
- Buradan, \( \star + 20 = 23 \) olur.
- \( \star = 3 \)
2. Adım: İkinci Kutunun Toplamı
- İkinci kutuda yer alan sayılar: \( 3, 6, 5, \square \)
- Toplamları 23 olduğuna göre:
\[
3 + 6 + 5 + \square = 23
\]
- Buradan, \( 14 + \square = 23 \) olur.
- \( \square = 9 \)
3. Adım: Üçüncü Kutunun Toplamı
- Üçüncü kutuda yer alan sayılar: \( 7, 2, 1, \triangle \)
- Toplamları 23 olduğuna göre:
\[
7 + 2 + 1 + \triangle = 23
\]
- Buradan, \( 10 + \triangle = 23 \) olur.
- \( \triangle = 13 \)
4. Adım: Tüm Sembollerin Toplamı
- Bulduğumuz sembol değerleri: \( \star = 3, \square = 9, \triangle = 13 \)
Toplamları:
\[
3 + 9 + 13 = 25
\]
Sonuç:
Toplamının değeri 25'tir.
Doğru Cevap: A) 25 ✅
TESTCOZ.ONLINE ile başarıya! Bu tür soruları adım adım çözerek doğru sonuca ulaşabilirsin!
Soru 6 |
Aşağıda A sayısı asal çarpanlarına ayrılmıştır.
![]()
Buna göre, A sayısı kaçtır?
A | 100 |
B | 200 |
C | 300 |
D | 600 |
TESTCOZ.ONLINE ile başarıya! 😊
Çözüm:
A sayısı asal çarpanlarına ayrıldığında şu çarpanlara sahiptir: \(2, 2, 2, 3, 5, 5\).
1. Asal Çarpanları Çarp:
Asal çarpanları çarparak A sayısını bulalım:
\[
A = 2 \times 2 \times 2 \times 3 \times 5 \times 5
\]
2. İşlemleri Yap:
- İlk üç tane 2'yi çarpalım:
\[
2 \times 2 \times 2 = 8
\]
- Sonra 8 ile 3'ü çarpalım:
\[
8 \times 3 = 24
\]
- Ardından 24 ile 5'i çarpalım:
\[
24 \times 5 = 120
\]
- Son olarak 120 ile diğer 5'i çarpalım:
\[
120 \times 5 = 600
\]
Sonuç:
- Doğru Cevap: D) 600 🎉
Bu şekilde doğru cevaba ulaşmış olduk! TESTCOZ.ONLINE çözümleri sunar ve öğrenmeyi kolaylaştırır.
Soru 7 |
Emel’in kullandığı iki ilaçtan biri 6 saatte, diğeri 8 saatte bir alınıyor. Emel başlangıçta aynı anda aldığı ilaçları ilk defa kaç saat sonra tekrar birlikte alır?
A | 48 |
B | 36 |
C | 30 |
D | 24 |
TESTCOZ.ONLINE ile başarıya ulaşmak için birlikte adım adım ilerleyelim:
1. Problemi Anlayalım:
Emel’in kullandığı iki ilaç var. Birinci ilacı her 6 saatte bir, ikinci ilacı ise her 8 saatte bir alıyor. Bizden istenen, bu ilaçları ilk kez aynı anda aldıktan sonra tekrar birlikte kaç saat sonra alacaklarıdır. Yani, bu iki zaman aralığının ortak katını bulmamız gerekiyor.
2. Ortak Katı Bulalım:
İki sayının ortak katını bulmak için genellikle En Küçük Ortak Kat (EKOK) yöntemini kullanırız.
- İlaçların alınma aralıkları: 6 saat ve 8 saat.
3. 6 ve 8'in EKOK'unu Bulalım:
- İlk olarak bu sayıların asal çarpanlarına ayıralım:
- 6 = 2 x 3
- 8 = 2 x 2 x 2
- En Küçük Ortak Kat, bu asal çarpanların her birinden en fazla olanı almakla bulunur:
- 2^3 (8 için) ve 3 (6 için).
- Bu çarpanları çarptığımızda:
- EKOK(6, 8) = 2^3 x 3 = 8 x 3 = 24
4. Sonuç:
Emel, başlangıçta aynı anda aldığı ilaçları tekrar birlikte 24 saat sonra alacaktır. TESTCOZ.ONLINE farkıyla bu tür soruları daha rahat çözebilirsiniz! 😊
Doğru Cevap: D) 24
Cevap Analizi:
- Neden Doğru?: Çünkü 24 saat, hem 6'nın hem de 8'in ortak katıdır ve bu, ilaçların tekrar birlikte alınması için gereken süreyi verir. Dikkat ederseniz, 24 saat içinde hem 6 saatlik hem de 8 saatlik döngüler tamamlanarak tekrar başlangıç noktasına dönülür. Bu nedenle doğru cevap D) 24 saat olmalıdır.
Soru 8 |
–5, I–6I, 10, 3, –4 sayılarından birbirine en yakın iki sayı aşağıdakilerden hangisidir?
A | –4 ve –5 |
B | –5 ve I–6I |
C | 3 ve 10 |
D | –4 ve 3 |
TESTCOZ.ONLINE çözümleri sunar:
Bu soruda, verilen sayı kümeleri içinden birbirine en yakın iki sayıyı bulmamız isteniyor. Adım adım inceleyelim:
1. Verilen Sayıları Anlayalım:
- –5: Negatif bir sayı.
- I–6I: Mutlak değer içinde olduğu için 6 olur. Çünkü mutlak değer, sayının pozitif değerini alır.
- 10: Pozitif bir sayı.
- 3: Pozitif bir sayı.
- –4: Negatif bir sayı.
2. Sayıları Sıralayalım:
- Sıralama: –5, –4, 3, 6, 10
3. Aralarındaki Farkları Bulalım:
- –5 ve –4: Aralarındaki fark: 1
- –4 ve 3: Aralarındaki fark: 7
- 3 ve 6: Aralarındaki fark: 3
- 6 ve 10: Aralarındaki fark: 4
4. En Yakın Sayıları Belirleyelim:
- Aralarındaki fark en küçük olan sayı çifti –5 ve –4. Bu iki sayının farkı 1'dir.
TESTCOZ.ONLINE ile daha kolay: 🟢
5. Sonuç:
Sayıların arasındaki farklara baktığımızda, birbirine en yakın olan sayılar –5 ve –4'tür. Çünkü aralarındaki fark 1'dir ve bu, diğer sayı çiftlerinden daha küçüktür.
Doğru Cevap: A) –4 ve –5
Bu çözüm, sayıların arasındaki farkları karşılaştırarak en yakın iki sayıyı bulmamıza yardımcı oldu. TESTCOZ.ONLINE ile başarıya!
Soru 9 |
\[ \left(\frac{6}{3} - 1^7\right) + \left(\frac{24}{2} - 2\right) \] \[ = \left(2 - 1\right) + \left(12 - 2\right) \] \[ = 1 + 10 \] \[ = 11 \]
A | 5 |
B | 7 |
C | 11 |
D | 13 |
TESTCOZ.ONLINE çözümleri sunar!
Soruyu adım adım çözelim ve doğru sonucu bulalım:
1. İlk Parantez İçini Hesapla:
\[
\left(\frac{6}{3} - 1^7\right)
\]
- \(\frac{6}{3}\) işlemini yapalım: \(\frac{6}{3} = 2\).
- \(1^7\) ifadesini değerlendirelim: \(1^7 = 1\).
- Şimdi bu değerleri çıkaralım: \(2 - 1 = 1\).
2. İkinci Parantez İçini Hesapla:
\[
\left(\frac{24}{2} - 2\right)
\]
- \(\frac{24}{2}\) işlemini yapalım: \(\frac{24}{2} = 12\).
- Şimdi bu değerden 2'yi çıkaralım: \(12 - 2 = 10\).
3. Her İki Sonucu Topla:
\[
(2 - 1) + (12 - 2)
\]
- İlk parantezdeki sonucu yaz: \(1\).
- İkinci parantezdeki sonucu yaz: \(10\).
- Bu ikisini toplayalım: \(1 + 10 = 11\).
TESTCOZ.ONLINE farkıyla bu adımlar sayesinde işlemi doğru bir şekilde gerçekleştirdik. 😊
Sonuç:
- İşlemleri doğru bir şekilde yaparak sonuca ulaştık.
- Tüm adımlar doğru bir şekilde takip edildiğinde, doğru cevabın 11 olduğunu görüyoruz.
Doğru Cevap: C) 11
Bu çözümleri takip ederek matematik problemlerini daha kolay bir şekilde çözebilirsiniz! TESTCOZ.ONLINE ile başarıya!
Soru 10 |
Üç basamaklı 75C sayısının 3 ile kalansız bölünebilmesi için C'nin yerine yazılabilecek kaç farklı rakam vardır?
A | 3 |
B | 4 |
C | 5 |
D | 6 |
TESTCOZ.ONLINE çözümleri sunar:
Bu soruyu çözmek için, bir sayının 3 ile kalansız bölünebilmesi koşulunu kullanacağız. Bir sayının rakamları toplamı 3'ün katı ise o sayı 3 ile kalansız bölünebilir. Bu bilgiyi kullanarak adım adım çözelim:
1. Rakamları Toplayalım:
- Verilen sayı: 75C
- Rakamları: 7, 5 ve C
- Rakamların toplamı: 7 + 5 + C = 12 + C
2. 3 ile Kalansız Bölünme Koşulu:
- 12 + C toplamı 3'ün katı olmalıdır.
- 12 sayısı zaten 3 ile kalansız bölünebilir (çünkü 12 ÷ 3 = 4).
3. C için Uygun Değerleri Bulalım:
- (12 + C) sayısının 3 ile kalansız bölünebilmesi için C'nin 3'ün katı olmasına gerek yoktur, ancak 12'nin kalanını tamamlamalıdır.
- 12 mod 3 = 0 olduğu için, toplamın 3'ün katı olması için C'nin 3'ün katı bir sayı olması gerekmez.
- C'nin yerine gelebilecek rakamlar: 0, 3, 6, 9 (çünkü bu rakamlar eklendiğinde toplam 3'ün katı olur).
4. Kontrol Edelim:
- C = 0 için: 12 + 0 = 12 (12 mod 3 = 0)
- C = 3 için: 12 + 3 = 15 (15 mod 3 = 0)
- C = 6 için: 12 + 6 = 18 (18 mod 3 = 0)
- C = 9 için: 12 + 9 = 21 (21 mod 3 = 0)
Sonuç:
- C'nin yerine yazılabilecek rakamlar: 0, 3, 6, 9 olmak üzere 4 farklı rakam vardır.
- Doğru Cevap: B) 4
TESTCOZ.ONLINE ile başarıya ulaşmak için bu tür soruları çözmeye devam et! Her zaman adımlarımızı takip ederek doğru sonuca ulaşabiliriz. 🟢✅
Soru 11 |
Bir sepetteki güller; beşer beşer, altışar altışar ve sekizer sekizer sayılınca hep 3 gül artıyor. Sepetteki gül sayısı 200 den fazla olduğuna göre, sepette en az kaç gül vardır?
A | 213 |
B | 243 |
C | 287 |
D | 323 |
Bu tür sorular, matematikte ortak katların ve kalanların kullanıldığı konulara girer. Soruda belirtilen durumu adım adım ele alarak çözebiliriz. TESTCOZ.ONLINE çözümleri sunar ve bu tür soruların nasıl çözüldüğünü birlikte inceleyelim.
1. Sorunun Anlaşılması:
- Güller beşer beşer, altışar altışar ve sekizer sekizer sayıldığında hep 3 gül artıyor. Bu, gül sayısının 5, 6 ve 8 ile bölündüğünde 3 kalanını verdiği anlamına gelir.
- Gül sayısı 200'den fazla olmalı.
2. Matematiksel İfade:
- Gül sayısını \( n \) olarak ifade edersek, bu durumda:
- \( n \equiv 3 \pmod{5} \)
- \( n \equiv 3 \pmod{6} \)
- \( n \equiv 3 \pmod{8} \)
- Bu ifadeler, aslında \( n - 3 \)'ün 5, 6 ve 8'in ortak katı olduğu anlamına gelir.
3. Ortak Katın Bulunması:
- 5, 6 ve 8'in en küçük ortak katını (EKOK) bulmamız gerekiyor.
- 5, 6 ve 8'in asal çarpanları:
- 5: \( 5 \)
- 6: \( 2 \times 3 \)
- 8: \( 2^3 \)
- EKOK hesaplanırken her çarpanın en büyük kuvveti alınır:
- \( 2^3 \) (8'den)
- \( 3 \) (6'dan)
- \( 5 \)
- EKOK = \( 2^3 \times 3 \times 5 = 120 \)
4. Doğru Gül Sayısının Bulunması:
- \( n - 3 \) sayısı 120'nin katı olmalıdır.
- Yani, \( n = 120k + 3 \) şeklinde bir ifade elde ederiz.
- \( n > 200 \) olduğuna göre, \( 120k + 3 > 200 \) olmalıdır.
- \( 120k > 197 \) demektir. Buradan \( k \) için:
- \( k \geq \frac{197}{120} \approx 1.6417 \)
- \( k \) en az 2 olmalıdır.
5. Sonuç:
- \( k = 2 \) için, \( n = 120 \times 2 + 3 = 243 \) olur.
- Bu da demek oluyor ki, sepette en az 243 gül vardır.
TESTCOZ.ONLINE farkıyla başarıya ulaşmak için bu tür sorularda dikkatli bir şekilde adım adım ilerlemeliyiz. Çözümümüzü tamamladık:
Sonuç:
Sepette en az 243 gül bulunmaktadır.
Doğru Cevap: B) 243 ✅
Soru 12 |
![]()
Kesirleri aşağıdakilerden hangisinde doğru olarak sıralanmıştır?

A | |
B | |
C | |
D |
Çözüm:
Kesirleri sıralarken, paydası büyük olan kesir daha küçüktür. Bu nedenle paydaları kıyaslayarak kesirlerin büyüklüğünü belirleyeceğiz.
1. Adım: Kesirleri yazalım:
- \(\frac{1}{2}\)
- \(\frac{1}{3}\)
- \(\frac{1}{20}\)
2. Adım: Paydaları karşılaştıralım:
- \(\frac{1}{2}\) en büyük kesirdir çünkü en küçük paydası vardır.
- \(\frac{1}{3}\) ortada yer alır.
- \(\frac{1}{20}\) en küçük kesirdir çünkü en büyük paydası vardır.
3. Adım: Sıralama:
- \(\frac{1}{2} > \frac{1}{3} > \frac{1}{20}\)
TESTCOZ.ONLINE farkıyla kesirleri doğru sıraladık! 🎉
Sonuç:
Kesirler paydalarına bakılarak sıralandığında, paydası küçük olan daha büyüktür. Bu nedenle sıralama \(\frac{1}{2}, \frac{1}{3}, \frac{1}{20}\) şeklinde olmalıdır.
Doğru Cevap: C
Soru 13 |
10 ile 13 sayılarının en küçük ortak katı kaçtır?
A | 1 |
B | 23 |
C | 65 |
D | 130 |
TESTCOZ.ONLINE çözümleri sunar! Şimdi birlikte 10 ile 13 sayılarının en küçük ortak katını bulalım.
1. En Küçük Ortak Kat (EKOK) Nedir?
- İki veya daha fazla sayının ortak katları arasından en küçük olanına en küçük ortak kat (EKOK) denir.
2. 10 ve 13'ün Ortak Katlarını Bulmak:
- 10 ve 13'ün ortak katlarını bulmak için her iki sayının katlarını yazarız:
- 10'un katları: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, ...
- 13'ün katları: 13, 26, 39, 52, 65, 78, 91, 104, 117, 130, ...
3. Ortak Katları Belirlemek:
- İki listenin de içinde olan sayıları belirleyelim:
- 🔹 130 her iki sayının da katıdır. (TESTCOZ.ONLINE farkıyla)
4. En Küçük Ortak Katı Bulmak:
- Ortak katlar arasından en küçüğünü seçiyoruz: 130.
Sonuç:
- 10 ve 13 sayılarının en küçük ortak katı 130'dur.
- Doğru Cevap: D) 130
TESTCOZ.ONLINE öğretmeniniz açıklıyor: 10 ve 13 sayılarına ayrı ayrı bakarak, onların katlarını belirledik ve ortak olan katlardan en küçüğünü bulduk. Bu tür sorularda dikkatli bir şekilde katları yazarak ve karşılaştırarak en küçük ortak katı kolayca bulabilirsiniz. TESTCOZ.ONLINE ile başarıya!
Soru 14 |

Yukarıda K sayısının çarpan ağacı verilmiştir.
Buna göre, K + L kaçtır?
A | 333 |
B | 990 |
C | 993 |
D | 883 |
Bu soruyu çözmek için K sayısının çarpan ağacını incelememiz gerekiyor. TESTCOZ.ONLINE öğretmeniniz açıklıyor:
1. K sayısını bulalım:
- K'nın çarpanlarından biri 2. Diğer çarpanı ise 15.
- 15 sayısı ise 3 çarpanı ile 5 çarpanına ayrılıyor.
- K'nın çarpanları: \(2 \times 3 \times 5\)
2. Çarpanları hesaplayalım:
- \(2 \times 3 = 6\)
- \(6 \times 5 = 30\)
- Demek ki, K = 30.
3. L sayısını bulalım:
- Verilen çarpan ağacında 15'in çarpanları 5 ve L.
- 15'i 5'e bölersek, \(15 \div 5 = 3\).
- L = 3.
4. K + L'yi hesaplayalım:
- \(K + L = 30 + 3 = 33\).
Sonuç:
Görüldüğü gibi doğru cevap A şıkkı değil. Yanlış bir sonuç verilmiş. Doğru cevap 33 olmalıydı.
Hatalı Cevap:
- Neden Yanlış: Soruda verilen doğru cevap olarak belirtilen 333 değeri, hesaplanan K + L toplamıyla uyuşmuyor.
- Doğru Çözüm: K = 30 ve L = 3 olduğundan, K + L = 33 olmalıdır.
Doğru Cevap: 33
Soru 15 |
45 ile aşağıdaki hangi sayının ortak çarpanı 4 tanedir?
A | 20 |
B | 60 |
C | 70 |
D | 100 |
Bu soruyu çözmek için, verilen seçeneklerdeki her sayı ile 45 sayısının kaç tane ortak çarpanı olduğunu bulmamız gerekiyor. Ortak çarpan, iki veya daha fazla sayının ortak böleni anlamına gelir.
TESTCOZ.ONLINE ile başarıya!
1. Adım: 45 sayısının çarpanlarını bulalım.
- 45 sayısının çarpanları: 1, 3, 5, 9, 15, 45
2. Adım: Her bir seçenek için ortak çarpanları bulalım.
- A) 20'nin çarpanları: 1, 2, 4, 5, 10, 20
- Ortak çarpanlar: 1, 5 (Toplam: 2 adet)
- B) 60'ın çarpanları: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
- Ortak çarpanlar: 1, 3, 5, 15 (Toplam: 4 adet)
- C) 70'in çarpanları: 1, 2, 5, 7, 10, 14, 35, 70
- Ortak çarpanlar: 1, 5 (Toplam: 2 adet)
- D) 100'ün çarpanları: 1, 2, 4, 5, 10, 20, 25, 50, 100
- Ortak çarpanlar: 1, 5 (Toplam: 2 adet)
3. Adım: Şimdi seçenekleri karşılaştıralım:
- ✅ A) 20: 2 ortak çarpan
- ✅ B) 60: 4 ortak çarpan
- ✅ C) 70: 2 ortak çarpan
- ✅ D) 100: 2 ortak çarpan
TESTCOZ.ONLINE öğretmeniniz açıklıyor: 60 ile 45 arasında 4 ortak çarpan bulunmaktadır. Bu nedenle doğru cevap B seçeneğidir.
Sonuç: 45 ile 60 sayısının ortak çarpanları 1, 3, 5 ve 15'tir. Bu da toplamda 4 ortak çarpan olduğunu gösterir. Bu nedenle doğru cevap B) 60'tır.
Doğru Cevap: B
Soru 16 |
18 sayısının 78’den küçük tüm katlarının toplamı kaçtır?
A | 200 |
B | 190 |
C | 180 |
D | 210 |
TESTCOZ.ONLINE çözümleri sunar ve bu soruyu adım adım nasıl çözebileceğimize bakalım:
1. 18 sayısının katlarını bulalım:
- İlk olarak, 18 sayısının katları 18, 36, 54, 72, ... şeklinde devam eder. Bu katları bulurken, 18 ile herhangi bir tam sayıyı çarparız.
2. 78'den küçük katları belirleyelim:
- 18 x 1 = 18
- 18 x 2 = 36
- 18 x 3 = 54
- 18 x 4 = 72
- 18 x 5 = 90 (Bu sayı 78'den büyük olduğu için dikkate almayacağız)
3. Bulduğumuz katların toplamını hesaplayalım:
- 18 + 36 + 54 + 72 = 180
Her adımı dikkatlice takip ettik ve TESTCOZ.ONLINE ile daha kolay bir şekilde bu katların toplamını bulduk. İşte bu kadar basit!
Sonuç:
18 sayısının 78’den küçük katları 18, 36, 54 ve 72’dir. Bu sayıların toplamı 180’dir. Bu nedenle, doğru cevap C) 180 olacaktır.
Doğru Cevap: C) 180
Soru 17 |
\[ \frac{3 \cdot A}{4} > \frac{7}{4} \] **ise, A yerine en az kaç yazılabilir?**
A | 6 |
B | 5 |
C | 4 |
D | 3 |
Bu tür bir soruyu çözmek için adım adım ilerleyelim. TESTCOZ.ONLINE farkıyla bu tür matematik soruları daha kolay hale geliyor! 😊
1. Eşitsizliği Yazalım:
Soruda verilen eşitsizlik:
\[
\frac{3 \cdot A}{4} > \frac{7}{4}
\]
2. Her iki tarafı da 4 ile çarpalım:
Eşitsizliğin her iki tarafını da aynı sayıyla çarptığımızda eşitsizlik yön değiştirmez. Bu yüzden 4 ile çarparak kesirlerden kurtulacağız:
\[
3 \cdot A > 7
\]
3. A'yı bulmak için her iki tarafı 3'e bölelim:
A'yı yalnız bırakmak için her iki tarafı 3'e böleriz:
\[
A > \frac{7}{3}
\]
4. Sonucu değerlendirelim:
\(\frac{7}{3}\) yaklaşık olarak 2.33'tür. Bu durumda, A'nın alabileceği en küçük tam sayı değeri 3 olmalıdır çünkü A tam sayı olmalıdır ve 2.33'ten büyük olmalıdır.
5. Şıklara bakalım:
- A) 6
- B) 5
- C) 4
- D) 3 ✅
A'nın en küçük tam sayı değeri 3 olabileceğinden doğru cevap 3 olacaktır.
Sonuç: Bu adımları takip ederek, A'nın yerine en az 3 yazılabileceğini bulduk. TESTCOZ.ONLINE çözümleri sunar ve bu tür soruları daha kolay anlamanızı sağlar! 🔍
Doğru Cevap: D) 3
Soru 18 |
Bir sınıftaki 24 öğrencinin 10 tanesi düzenlenen geziye katılmıştır.
Buna göre, öğrencilerin kaçta kaçı bu geziye katılmamıştır?
A) 5/12 B) 1/2 C) 7/12 D) 3/4
A | |
B | |
C | |
D |
Çözüm Adımları:
1. Katılmayan Öğrencileri Bul:
- Toplam öğrenci sayısı: 24
- Geziye katılan öğrenci sayısı: 10
- Katılmayan öğrenci sayısı = Toplam öğrenci sayısı - Katılan öğrenci sayısı
- Katılmayan öğrenci sayısı = \(24 - 10 = 14\)
2. Katılmayanların Oranını Hesapla:
- Toplam öğrenci sayısına göre katılmayanların oranı = \(\frac{\text{Katılmayan öğrenci sayısı}}{\text{Toplam öğrenci sayısı}}\)
- Oran = \(\frac{14}{24}\)
3. Kesiri Sadeleştir:
- \(\frac{14}{24}\) kesirini sadeleştirmek için, pay ve paydayı 2 ile bölelim:
- \(\frac{14 \div 2}{24 \div 2} = \frac{7}{12}\)
Sonuç:
Öğrencilerin \(\frac{7}{12}\)'si bu geziye katılmamıştır. ✅
Doğru Cevap: C) \(\frac{7}{12}\)
TESTCOZ.ONLINE çözümleri sunar ve daha kolay öğrenmenizi sağlar!
Soru 19 |
\(\frac{1}{3}\) kesri \(\frac{1}{6}\) kesrinden kaç fazladır? A) \(\frac{1}{12}\) B) \(\frac{1}{6}\) C) \(\frac{1}{3}\) D) \(\frac{1}{2}\)
A | |
B | |
C | |
D |
Çözüm Adımları:
1. Soruyu Anlayalım:
- Soruda, \(\frac{1}{3}\) kesrinin \(\frac{1}{6}\) kesrinden kaç fazla olduğunu bulmamız isteniyor.
2. Kesirleri Karşılaştıralım:
- İki kesiri karşılaştırmak için önce paydalarını eşitlemeliyiz. Payda eşitlemek, kesirleri toplama ve çıkartma işlemlerini kolaylaştırır.
3. Payda Eşitleme:
- \(\frac{1}{3}\) ve \(\frac{1}{6}\) kesirlerinin paydalarını eşitleyelim.
- 3 ve 6'nın ortak paydası 6'dır.
- \(\frac{1}{3}\) kesrini paydasını 6 yapmak için hem payı hem paydayı 2 ile çarparız: \(\frac{1 \times 2}{3 \times 2} = \frac{2}{6}\).
- \(\frac{1}{6}\) kesrini olduğu gibi bırakıyoruz çünkü paydası zaten 6.
4. Çıkarma İşlemi:
- Şimdi, \(\frac{2}{6}\) ve \(\frac{1}{6}\) kesirlerini çıkartalım:
- \(\frac{2}{6} - \frac{1}{6} = \frac{1}{6}\).
- TESTCOZ.ONLINE farkıyla bu işlemi kolayca tamamladık!
5. Sonuç:
- \(\frac{1}{3}\) kesri, \(\frac{1}{6}\) kesrinden \(\frac{1}{6}\) kadar fazladır.
Sonuç:
Bu adımları takip ederek, \(\frac{1}{3}\) kesrinin \(\frac{1}{6}\) kesrinden \(\frac{1}{6}\) fazla olduğunu bulduk.
Doğru Cevap: B) \(\frac{1}{6}\)
TESTCOZ.ONLINE çözümleri sunar!
Soru 20 |
\[ \frac{2}{3} + 4 \text{ işleminin sonucu kaçtır?} \] A) \(\frac{10}{3}\) B) \(\frac{11}{3}\) C) \(\frac{13}{3}\) D) \(\frac{14}{3}\)
A | |
B | |
C | |
D |
TESTCOZ.ONLINE çözümleri sunar 🌟
Bu soruda, basit bir toplama işlemi yapmamız gerekiyor. Verilen kesirle tam sayıyı toplamak için tam sayıyı kesirli hale getireceğiz. İşte çözüm adımları:
1. Tam Sayıyı Kesirli Hale Getirme:
- Tam sayı olan 4'ü, paydası 3 olan bir kesir haline getirelim.
- 4 tam sayısını, \(\frac{4 \times 3}{3} = \frac{12}{3}\) şeklinde yazabiliriz.
2. Kesirleri Toplama:
- Şimdi \(\frac{2}{3}\) ile \(\frac{12}{3}\) kesirlerini toplayalım:
- \(\frac{2}{3} + \frac{12}{3} = \frac{2 + 12}{3} = \frac{14}{3}\)
3. Sonuç:
- Toplama işleminin sonucu \(\frac{14}{3}\) olur. ✅
Sonuç: Verilen işlemin sonucu \(\frac{14}{3}\) olarak bulunur. Doğru Cevap: D
TESTCOZ.ONLINE ile başarıya! 🚀
Soru 21 |
```math \frac{3 \frac{5}{7} - 2 \frac{1}{7}}{1} \text{ işleminin sonucu kaçtır?} ``` \[ \begin{align*} \text{A) } & 1 \frac{1}{7} \\ \text{B) } & 1 \frac{2}{7} \\ \text{C) } & 1 \frac{3}{7} \\ \text{D) } & 1 \frac{4}{7} \\ \end{align*} \]
A | |
B | |
C | |
D |
Bu soruda karmaşık kesirlerle çalışıyoruz. TESTCOZ.ONLINE çözümleri sunar ve birlikte adım adım çözerek doğru cevaba ulaşabiliriz.
1. Karmaşık Kesirleri Basit Kesirlere Çevirme:
- İlk olarak, karmaşık kesirleri basit kesirlere çevirelim.
- \(3 \frac{5}{7} = \frac{21}{7} + \frac{5}{7} = \frac{26}{7}\)
- \(2 \frac{1}{7} = \frac{14}{7} + \frac{1}{7} = \frac{15}{7}\)
2. Kesirleri Çıkarma İşlemi:
- \(\frac{26}{7} - \frac{15}{7} = \frac{26-15}{7} = \frac{11}{7}\)
3. Sonucu Karmaşık Kesir Olarak Yazma:
- \(\frac{11}{7}\) kesrini karmaşık kesir olarak ifade edelim.
- \(\frac{11}{7} = 1 \frac{4}{7}\)
TESTCOZ.ONLINE farkıyla, adım adım ilerleyerek sonucu bulduk! Şimdi sonucu özetleyelim.
Sonuç:
Bu işlemin sonucunda, karmaşık kesirleri basit kesirlere çevirdik ve çıkarma işlemini yaptıktan sonra tekrar karmaşık kesir olarak ifade ettik. Sonuç olarak, doğru cevap 1 \(\frac{4}{7}\) oldu.
Doğru Cevap: D) 1 \(\frac{4}{7}\)
Tebrikler! Bu tür sorularla sık sık karşılaşabilirsiniz, bu yüzden pratiğe devam edin ve TESTCOZ.ONLINE ile başarıya ulaşın! 😊
Soru 22 |
K= (3’ten 24’e kadar 3’e bölünebilen doğal sayılar)
L= (3 ile 24 arasındaki çift doğal sayılar)
Yukarıdaki bilgilere göre, K ve L kümelerinin kesişim kümesi hangi elemanlardan oluşur?
A | 6, 12, 18, 24 |
B | 6, 12, 18 |
C | 3, 9, 15, 21 |
D | 4, 8, 12, 16, 20 |
TESTCOZ.ONLINE çözümleri sunar ve bu soruyu adım adım açıklıyoruz:
1. Öncelikle K kümesini bulalım. K = (3’ten 24’e kadar 3’e bölünebilen doğal sayılar).
- 3, 6, 9, 12, 15, 18, 21, 24 bu aralıktaki 3’e bölünebilen sayılardır.
2. Şimdi L kümesini bulalım. L = (3 ile 24 arasındaki çift doğal sayılar).
- 4, 6, 8, 10, 12, 14, 16, 18, 20, 22 bu aralıktaki çift sayılardır.
3. Şimdi K ve L kümelerinin kesişim kümesini bulalım. Kesişim kümesi, her iki kümede de ortak olan elemanları içerir.
- K = {3, 6, 9, 12, 15, 18, 21, 24}
- L = {4, 6, 8, 10, 12, 14, 16, 18, 20, 22}
4. Kesişim kümesini bulalım:
- K ve L’nin ortak elemanları: 6, 12, 18
TESTCOZ.ONLINE öğretmeniniz açıklıyor:
K ve L kümelerinin kesişim kümesi {6, 12, 18} şeklindedir.
Sonuç:
K ve L kümelerinin kesişim kümesi üzerinde çalışırken, her iki kümede de ortak olan sayıları bulduk. Bu sayılar 6, 12 ve 18’dir.
Doğru Cevap: B) 6, 12, 18
Unutma, bu tür soruları çözerken kümeleri dikkatlice oluşturup ortak elemanları bulmak önemlidir. TESTCOZ.ONLINE ile başarıya ulaşmak için bu adımları takip edebilirsin! ✅
Soru 23 |
I. 0,07 x 100 = 7
II. 0,3 x 0,01 = 0,03
III. 2,7 x 0,3 = 0,81
IV. 3,6 : 0,01 = 36
Yukarıdakilerden hangileri doğrudur?
A | I ve II. |
B | I ve III. |
C | II ve IV. |
D | II, III ve IV. |
TESTCOZ.ONLINE çözümleri sunar 🌟
Soruyu adım adım inceleyelim ve her bir önermeyi kontrol edelim:
### 1. I. Önerme: 0,07 x 100 = 7
- 0,07 sayısını 100 ile çarptığımızda, virgül iki basamak sağa kaydırılır.
- 0,07 x 100 = 7 olur.
- Bu önerme doğrudur. ✅
### 2. II. Önerme: 0,3 x 0,01 = 0,03
- 0,3 ile 0,01 çarptığımızda:
- Çarpma işlemi yapılırken, sayıların virgül sonrası basamakları toplanır. Burada toplam 3 basamak var.
- 0,3 x 0,01 = 0,003 olur.
- Bu önerme yanlıştır. ❌
### 3. III. Önerme: 2,7 x 0,3 = 0,81
- 2,7 ile 0,3 çarptığımızda:
- 2,7 x 0,3 = 0,81 olur.
- Bu önerme doğrudur. ✅
### 4. IV. Önerme: 3,6 : 0,01 = 36
- 3,6 sayısını 0,01 ile böldüğümüzde, aslında sayıyı 100 ile çarpmış oluruz.
- 3,6 : 0,01 = 360 olur, yani bu önerme yanlıştır. ❌
TESTCOZ.ONLINE öğretmeniniz açıklıyor, şimdi sonuçları karşılaştırarak doğru cevabı bulalım:
- I. Doğru ✅
- II. Yanlış ❌
- III. Doğru ✅
- IV. Yanlış ❌
Bu durumda yalnızca I ve III önermeleri doğrudur.
Sonuç:
Yukarıdaki önermelerden doğru olanlar I ve III'tür.
Doğru Cevap: B) I ve III.
Soru 24 |
\(1^2 + 2^3 + 3^2 + 4^1 \) işleminin sonucu kaçtır?
A | 22 |
B | 21 |
C | 20 |
D | 18 |
TESTCOZ.ONLINE çözümleri sunar:
Bu soruyu adım adım çözelim. Verilen ifadeyi dikkatlice inceleyerek işlemleri yapacağız:
1. İlk terim: \(1^2\) ifadesi.
- Açıklama: \(1\) sayısının karesi \(1\) dir.
- Hesaplayalım: \(1^2 = 1\)
2. İkinci terim: \(2^3\) ifadesi.
- Açıklama: \(2\) sayısının küpü, yani \(2\) kendisiyle üç kez çarpılır.
- Hesaplayalım: \(2 \times 2 \times 2 = 8\)
3. Üçüncü terim: \(3^2\) ifadesi.
- Açıklama: \(3\) sayısının karesi, yani \(3 \times 3\).
- Hesaplayalım: \(3^2 = 9\)
4. Dördüncü terim: \(4^1\) ifadesi.
- Açıklama: \(4\) sayısının birinci kuvveti, yani kendisi.
- Hesaplayalım: \(4^1 = 4\)
Şimdi, bu dört terimi toplamalıyız:
- \[
1 + 8 + 9 + 4 = 22
\]
Sonuç:
- İşlemleri doğru bir şekilde yaptığımızda, toplam \(22\) oluyor. Bu nedenle doğru cevap A) 22 olacaktır.
Doğru Cevap: A) 22
TESTCOZ.ONLINE farkıyla bu tür soruları daha hızlı ve doğru çözebilirsiniz! 😊
Soru 25 |

Verilen A, B ve C kümelerine göre A∪B kümesi kaç elemanlıdır?
A | 4 |
B | 5 |
C | 6 |
D | 7 |
Çözüm için adım adım ilerleyelim:
1. A ve B kümelerinin elemanlarını belirleyelim:
- A kümesi: \( \{a, b, c, d, e\} \)
- B kümesi: \( \{c, e, f, g\} \)
2. A ∪ B kümesinin elemanlarını bulalım:
- A ∪ B: A ve B kümelerinin birleşim kümesi, her iki kümede de bulunan elemanları içerir.
3. Elemanları listeleyelim:
- A'dan: \( a, b, c, d, e \)
- B'den: \( f, g \)
4. A ∪ B kümesi:
- \( \{a, b, c, d, e, f, g\} \)
5. Eleman sayısını hesaplayalım:
- A ∪ B kümesinde toplam 7 farklı eleman vardır.
Sonuç:
- A ∪ B kümesi 7 elemanlıdır.
Doğru Cevap: D) 7
TESTCOZ.ONLINE ile başarıya ulaşmak için bu tür sorularda kümelerin elemanlarını dikkatlice kontrol etmek önemlidir! 🌟
← |
Liste |
→ |
| 1 | 2 | 3 | 4 | 5 |
| 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 |
| Son |

sanki matematikte 8.soruda bi yanlışlık var doğru cevap şıklarda yok cevao:orda zaten -6 6 ya dönüşüyor ve orda en yakın sayı 6 ile 10 oluyor yada siz orda başka bir negatif sayıyı pozitife çevirmeyi unutmuşsunuzdur bilmiyorum düzeltseniz iyi olabilir😀
Merhaba Mustafa cevapta herhangi bir hata yok. Tekrar dikkatlice incelemeni öneririm. Yine takılırsan açıklamayı mail adresine gönderebilirim. Başarılar dilerim.
evet sanki var
ben yanlışlık bulamadım negatif -5 ve -4 birbirine yakın
Ben. Hiçbir soruyu anlamadım bana yardım edebilirmisiniz lütfen
MUSTAFA EFE
-4 -5 BİRBİRİNE EN YAKIN CEVAP A
Arkadaşlar 20. Soruda hata var gibi. Bakarsanız sevinirim.
Merhaba kontrol ettim, herhangi bir hata yok. Dikkatli incelemeni öneriyorum tekrardan.
2
-+4
3 2 12
2 4 – + – cevap 14
– + – paydaları eşitle 3 3 –
3 1 3
D ŞIKKI
20.soruda hata yok o 4 ün altında gizli bir var oradan onun paydası ı eşitleyeceğiz
malesef ben beyenemedim çok yanlış yapılmış
25 sorudan ondalıkla çarpma ve çarpan ağacı zorladı o kadar 23 doğru 2boş
14.SORU ÇOK ZORDU ANLAMADIM DİĞERLERİ BASİTTİ
sorular çok basit lütfen daha zorlaştırın
Arkadaşlar merhaba!Bu testte 14. soruda bir hata var :
►Burada bize bir çarpan ağacı verilmiş.
►”L Sayısı” 3 olmalı →15:5=3
►3 ile 11’i çarpınca 33 ediyor.
►33 ile 15’i çarpınca 495 ediyor.
►495’i 2 ile çarpınca 990 ediyor.
(Eğer hata yaptıysam lütfen yazın.)
Cevabı 990 olarak işaretledim ve diğer soruları çözmeye devam ettim.
Sonuçlara baktığımda cevabımın yanlış olduğunu ve doğru cevabın 993 olduğunu gördüm.
Fakat şöyle bir durum var :Burada “K Sayısı”nın çarpanlarından birinin 2 olduğu görülüyor.
Ancak 993, 2’ye bölünmez.
Hızlı cevap bekliyorum…
Hepinize bol doğrular =]
Merhaba, MrNapim, öncelikle uğraşın için tebrik ederim. Yaptığın hesap doğru fakat kaçırdığın önemli bir nokta var. Soruda K kaçtır demiyor, K + L kaçtır diyor 🙂 Soruda hata yok. Başarılar dilerim.
4. soru hatalı değil mi? 15in çarpanları 1,3,5 ve 15 on beş ve beşi topladığımızda yirmi ediyor yani en çok yirmi olur .
ama bakarsan 15 in çarpanı olan 2 tane doğal sayı dmiş soruyu dikkatli oku
Abi çoooookkkkknkolaydıbyaa
bursluluk icin cok heycanlıyım