6. Sınıf Matematik 2. Dönem 2. Yazılı Soruları
Tebrikler! 6. Sınıf Matematik 2. Dönem 2. Yazılı Soruları adlı sınavı başarıyla tamamladınız.
→ Toplam soru sayısı: %%TOTAL%%
→ Doğru sayınız: %%SCORE%% - yanlış ve boş sayınız: %%WRONG_ANSWERS%%.
→ Sınavdan aldığınız puan: %%PERCENTAGE%%
→ Sınav sonucu değerlendirmeniz: %%RATING%%
Soru 1 |
Aşağıdakilerden hangisi iki veri grubunu karşılaştırmayı gerektiren bir araştırma sorusudur?
Ülkemize gelen yabancı turistlerin en çok tercih ettiği iller hangileridir? | |
En çok sevilen pasta türü hangisidir? | |
Sınıfımızda kız ve erkek öğrencilerin sevdikleri renkler nelerdir? | |
Kız öğrencilerin en sevdiği hayvan türü nedir? |
Soru 2 |
Üç sayının aritmetik ortalaması 40 tır. Bu sayılardan iki tanesi 20 ve 55 ise diğer sayı kaçtır?
35 | |
40 | |
45 | |
50 |
Soru 3 |
Bir torbada bulunan topların 12 tanesi mavi, 8 tanesi yeşildir.
Buna göre bu torbadaki yeşil topların sayısının tüm topların sayısına oranı aşağıdakilerden hangisidir?
$$\frac{2}{3}$$ | |
$$\frac{3}{2}$$ | |
$$\frac{2}{5}$$ | |
$$\frac{3}{5}$$ |
Soru 4 |
Aşağıdaki cebirsel ifadelerden hangisi “Bir sayının 9 fazlasının yarısı” ifadesine karşılık gelir?
$$\frac{x}{9}+2$$ | |
$${x+2}\over{9}$$ | |
$$\frac{x}{2}+9$$ | |
$${x+9}\over{2}$$ |
Soru 5 |
$$2x-1\over{5}$$
Yukarıda verilen cebirsel ifadenin x = 18 için değeri kaçtır?
6 | |
7 | |
8 | |
9 |
Soru 6 |
Tümleri 40° olan açının bütünleri kaç derecedir?
120 | |
130 | |
140 | |
150 |
Soru 7 |
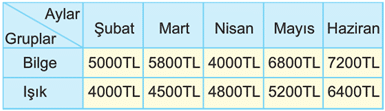
Tabloda, iki grubun aylara göre kazançları verilmiştir.
Buna göre aşağıdakilerden hangisi yanlıştır?
Bilge grubunun en çok kazandığı ay hazirandır. | |
Işık grubunun kazancı her ay artmıştır. | |
Işık grubunun en az kazandığı ay şubattır. | |
Bilge grubunun en az kazandığı ay şubattır. |
Soru 8 |
Yukarıda kare içinde verilen çember, karenin kenarlarına değmektedir.
Karenin çevresi 80 cm olduğuna göre çemberin yarıçapı kaç cm'dir?
5 | |
10 | |
20 | |
40 |
Soru 9 |
Yukarıda verilen bir ayrıtının uzunluğu 5 cm olan küplerden oluşturulmuş yapının hacmi kaç cm³ tür?
400 | |
450 | |
500 | |
550 |
Soru 10 |
Yukarıda verilen kare prizmanın hacmi 360 cm3 ise yüksekliği kaç cm'dir?
8 | |
9 | |
10 | |
11 |
Soru 11 |
Yukarıda verilen eş küplerden oluşturulmuş yapının hacmi kaç birim küptür?
23 | |
24 | |
25 | |
26 |
Soru 12 |
Yukarıda verilen eş küplerden oluşturulmuş prizmanın hacmi kaç birim küptür?
25 | |
30 | |
35 | |
40 |
Soru 13 |
Yarıçapının uzunluğu 10 cm olan çemberin uzunluğu kaç cm'dir? (π=3 alınız.)
40 | |
50 | |
60 | |
70 |
Soru 14 |
Dikdörtgenler prizmasının köşe sayısı A, ayrıt sayısı B ve yüzey sayısı C olduğuna göre A + B – C işleminin sonucu kaçtır?
11 | |
12 | |
13 | |
14 |
Soru 15 |
Aşağıda verilen eşitliklerden hangisi yanlıştır?
3 dam2 = 300 m2 | |
0,7 km2 = 70 000 m2 | |
14 m2 = 140 000 cm2 | |
0,52 cm2 = 52 mm2 |
Soru 16 |
Aşağıda verilen eşitliklerden hangisi yanlıştır?
1 hektar = 10 dekar | |
3 dönüm = 3000 m2 | |
800 dekar = 8 ar | |
5 hektar = 50000 m2 |
Soru 17 |
Bir arsanın alanı 15 ardır. Bu arsanın 350 m2 lik kısmına ev, 250 m2 lik kısmına ise havuz yapılacaktır.
Buna göre geriye kaç m2 boş alan kalır?
600 | |
700 | |
800 | |
900 |
Soru 18 |
Bir tenceredeki 5 L komposto, her biri 250 mL olan kâselere dökülerek servis edilecektir.
Buna göre kaç kâse gereklidir?
10 | |
20 | |
50 | |
100 |
Soru 19 |
Yukarıda verilen ABC üçgeninde,
[AB] ⊥ [BC] |BC|=15 cm'dir.
ABC üçgeninin alanı 75 cm² olduğuna göre, |AB| kaç cm'dir?
8 | |
9 | |
10 | |
12 |
Soru 20 |
Yukarıdaki şekilde kırmızı üçgenin alanı 18 cm², dikdörtgenin alanı 180 cm² olduğuna göre, aşağıdaki yorumlardan hangisi yanlıştır?
Kırmızı üçgenin yüksekliği |AH|=12 cm'dir | |
|HC|=15 cm'dir. | |
Paralelkenarın alanı 198 cm²'dir. | |
Mavi üçgenin alanı, kırmızı üçgenin alanına eşittir. |
| Liste |
EN İYİNİN DE İYİSİ
BEST IN THE BEST
yapana helal olsun adam gibi adam onun sayesinde 90 aldım
Soruların aynısımı çıktı yoksa benzerlerimi