KPSS Matematik Deneme Sınavı 5
Tebrikler! KPSS Matematik Deneme Sınavı 5 adlı sınavı başarıyla tamamladınız.
→ Toplam soru sayısı: %%TOTAL%%
→ Doğru sayınız: %%SCORE%% - yanlış ve boş sayınız: %%WRONG_ANSWERS%%.
→ Sınavdan aldığınız başarı yüzdesi: %%PERCENTAGE%%
→ Sınav sonucu değerlendirmeniz: %%RATING%%
Soru 1 |
A = 6 . 8 . 10 + 8 . 10 . 12 + ... + 22 . 24 . 26 olduğuna göre,
2 . 3 . 4 + 3 . 4 . 5 + ... + 11 . 12 . 13
ifadesinin A'türünden eşiti aşağıdakilerden hangisidir?
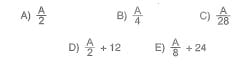
Soru 2 |
Aba aab ve bab üç basamaklı doğal sayılardır.
aba+aab+bab=1108 olduğuna göre a-b kaçtır ?
0 | |
1 | |
2 | |
3 | |
14 |
Soru 3 |
Ardışık 7 tam sayının toplamı, bu sayılardan en küçüğünün 5 katından 45 fazladır.
Buna göre, bu sayılardan en büyüğü kaçtır?
17 | |
18 | |
19 | |
20 | |
21 |
Soru 4 |
a, b, c birer tam sayı olmak üzere,
2a + b ve 3b + 5c birer tek sayı olduğuna göre,
I. a + b + c çifttir.
II. a . b . c çifttir.
III. a . b + c tektir.
ifadelerinden hangileri kesinlikle doğrudur?
Yalnız I | |
Yalnız II | |
I ve II | |
II ve III | |
I, II ve III |
Soru 5 |
3x5y dört basamaklı bir doğal sayıdır.
Bir kişi tanesi 36 TL olan kazaklardan a tane almış ve toplam 3x5y TL ödemiştir.
Buna göre a'nın alabileceği en büyük değer kaçtır?
96 | |
102 | |
103 | |
105 | |
107 |
Soru 6 |

Soru 7 |

Soru 8 |
x sayısının sayı doğrusunda -3 sayısına olan uzaklığı A dır.
-3 sayısının sayı doğrusunda x sayısına olan uzaklığı B dir.
A + B = 8
olduğuna göre, x’in alabileceği farklı değerlerin toplamı kaçtır ?
-6 | |
-3 | |
0 | |
3 | |
6 |
Soru 9 |
a ve b sıfırdan ve birbirinden farklı gerçel sayılar olmak üzere,
a³ < a² - b² < b
olduğuna göre,
I. a < 1
II. O < b < 1
![]()
ifadelerinden hangileri her zaman doğrudur?
I ve II | |
I ve III | |
II ve III | |
Yalnız II | |
Yalnız I |
Soru 10 |
m ve n birer gerçel sayı olmak üzere,

olduğuna göre, m kaçtır?
3 | |
4 | |
5 | |
6 | |
7 |
Soru 11 |
Gerçel sayılarda tanımlı f ve g fonksiyonları
f(x + 2) = f(x) + 8
g(x — 1) = 2x + 3
eşitliklerini sağlıyor.
f(8) + g(5) = 25
olduğuna göre, f(10). g(3) değeri kaçtır?
160 | |
175 | |
184 | |
198 | |
204 |
Soru 12 |

6 | |
5 | |
4 | |
3 | |
2 |
Soru 13 |
x ve y birer asal sayı, z bir pozitif çift doğal sayıdır.
x² - y² = z
olduğuna göre, x + y + z toplamının en küçük değeri kaçtır?
20 | |
24 | |
26 | |
28 | |
32 |
Soru 14 |
![]()
eşitsizliğini sağlayan kaç farklı x tam sayısı vardır?
4 | |
5 | |
6 | |
7 | |
8 |
Soru 15 |
x bir pozitif gerçel sayı olmak üzere,
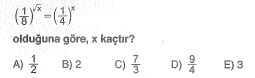
Soru 16 |
Bir kafede içinde sadece kaşar peyniri ve sucuk bulunan pizzalar satılmaktadır. Bu pizzalar ile ilgili aşağıdakiler bilinmektedir.
Pizzalar küçük ve büyük boy olmak üzere iki farklı büyüklükte hazırlanmaktadır.
Her bir pizza hazırlanırken kullanılan kaşar peyniri miktarının sucuk miktarına oranı sabittir.
Kullanılan kaşar peyniri ve sucuk miktarlarının toplamı küçük boy pizzalarda 180 gram ve büyük boy pizzalarda 225 gramdır.
Bu kafe de 1 küçük ve 1 büyük boy pizza hazırlanmış ve bu pizzalar için toplam 225 gram sucuk kullanılmıştır.
Buna göre; büyük boy pizzada kullanılan kaşar peyniri miktarı, küçük boy pizzada kullanılan kaşar peyniri miktarından kaç gram daha fazladır?
15 | |
20 | |
25 | |
30 | |
35 |
Soru 17 |
A ve B aynı evrensel kümenin iki alt kümesidir.
[(A' n B) u (B' n A)] u (A n B)
ifadesi aşağıdakilerden hangisine eşittir?
A | |
B | |
A U B | |
E | |
ø |
Soru 18 |
Aralıksız çalışarak bir yüzeye sıva yapıp seramik döşemek isteyen bir usta yaptığı iş planında belirlediği çalışma süresinin %25'ini sıva işine, kalan sürenin tamamını ise seramik döşeme işine ayırmıştır. Ancak, işin tamamını planladığı süreden %20 daha kısa sürede bitiren bu usta çalıştığı sürenin %40'ında sıva yapmış ve kalan süresini seramik döşeme işine ayırmıştır
Buna göre, bu usta seramik döşeme işine planladığından yüzde kaç daha az süre ayırmıştır?
36 | |
35 | |
32 | |
30 | |
28 |
Soru 19 |
A kentinden B kentine doğru saatte 100 ve 80 kilometre sabit hızlarla aynı anda harekete başlayan iki araçtan hızlı olanı bir süre sonra bozulmuş ve tamir için 2 saat durmak zorunda kaldıktan sonra başlangıçtaki sabit hızıyla kaldığı yerden yoluna devam etmiştir.
Hızlı olan araç B kentine diğer araçtan yarım saat sonra ulaştığına göre, yavaş olan araç A kentinden B kentine kaç saatte gitmiştir?
![]()
Soru 20 |
Bir annenin yaşı, üçer yıl arayla doğmuş 4 çocuğunun yaşları toplamına eşittir.
4 yıl sonra annenin yaşı, yaşça en büyük olan çocuğunun yaşının 2 katından 10 fazla olacağına göre, en küçük çocuğun bugünkü yaşı kaçtır?
7 | |
8 | |
9 | |
10 | |
11 |
Soru 21 |
51. ve 52. Soruları Aşağıdaki Bilgiye Göre Birbirinden Bağımsız Olarak Cevaplayınız.
Bir mağazada 2019 ve 2020 yıllarında satılan A ve B ürünlerinin sayıca dağılımı aşağıdaki daire grafiklerinde verilmiştir.
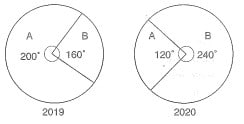
Bu mağazada 2020 yılında satılan A ve B ürünlerinin sayılarının toplamı, 2019 yılına göre %25 artmıştır.
2019 ve 2020 yıllarında satılan A ürünlerinin sayıları toplamı 1750 olduğuna göre, 2020 yılında satılan B ürünü sayısı kaçtır?
1000 | |
1050 | |
1250 | |
1400 | |
1500 |
Soru 22 |
51. ve 52. Soruları Aşağıdaki Bilgiye Göre Birbirinden Bağımsız Olarak Cevaplayınız.
Bir mağazada 2019 ve 2020 yıllarında satılan A ve B ürünlerinin sayıca dağılımı aşağıdaki daire grafiklerinde verilmiştir.

Bu mağazada 2020 yılında satılan A ve B ürünlerinin sayılarının toplamı, 2019 yılına göre %25 artmıştır.
2020 yılında satılan B ürünlerinin sayısı, 2019 yılında satılan A ürünlerinin sayısının 2 katından 700 azdır.
Buna göre, 2019 ve 2020 yıllarında satılan A ve B ürünlerinin sayıları toplamı kaçtır?
5230 | |
5670 | |
6080 | |
6225 | |
7185 |
Soru 23 |
53. ve 54. Soruları Aşağıdaki Bilgiye Göre Birbirinden Bağımsız Olarak Cevaplayınız.
Güven Öğretmen, matematik dersinde tahtaya 1'den 12'ye kadar olan 12 tam sayıyı yazmış ve öğrencilerinden her adımda tahtada yazılı olan sayılardan birini seçerek seçilen sayı çift ise bu sayıyı tam bölen tüm sayıları, tek ise bu sayıdan büyük olan tüm çift sayıları tahtadan silmelerini istemiştir.
Güven Öğretmen birinci adımda 8, ikinci adımda 9 ve üçüncü adımda ise 6 sayısını seçmiştir.
Buna göre, bu üç adımdan sonra tahtada kalan sayıların toplamı kaçtır?
20 | |
24 | |
27 | |
32 | |
35 |
Soru 24 |
53. ve 54. Soruları Aşağıdaki Bilgiye Göre Birbirinden Bağımsız Olarak Cevaplayınız.
Güven Öğretmen, matematik dersinde tahtaya 1'den 12'ye kadar olan 12 tam sayıyı yazmış ve öğrencilerinden her adımda tahtada yazılı olan sayılardan birini seçerek seçilen sayı çift ise bu sayıyı tam bölen tüm sayıları, tek ise bu sayıdan büyük olan tüm çift sayıları tahtadan silmelerini istemiştir.
Üç adımın uygulandığı durumda Güven Öğretmen'in birinci adımdan sonra seçtiği her bir sayı, bir önceki ![]() katıdır.
katıdır.
Buna göre, üçüncü adımdan sonra tahtada kalan sayıların toplamı en az kaçtır?
32 | |
35 | |
40 | |
42 | |
47 |
Soru 25 |
Erol, Birol ve Sinem bir futbol topu almak istemektedir. Alacakları futbol topunun fiyatı ile ilgili aşağıdakiler bilinmektedir.
• Erol’un parasından 40 TL fazladır.
• Birol'un parasının ![]() ü kadardır.
ü kadardır.
• Sinem'in parasının ![]() ünden 70 TL daha fazladır.
ünden 70 TL daha fazladır.
Üçü paralarını birleştirerek bu futbol topunu aldıklarında 206 TL para arttığına göre, Erol'un parası kac TL'dir?
150 | |
120 | |
96 | |
80 | |
72 |
Soru 26 |
Biri mavi diğeri kırmızı olan iki zar birlikle atılıyor.
Mavi zarın üst yüzüne gelen sayının kırmızı zarın üst yüzüne gelen sayıdan büyük olma olasılığı kaçtır?
![]()
Soru 27 |
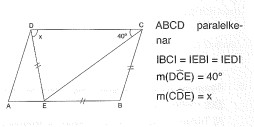
Yukarıdaki verilere göre, x kaç derecedir?
60 | |
65 | |
70 | |
75 | |
80 |
Soru 28 |
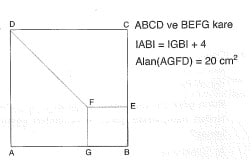
Yukarıdaki verilere göre, |AB| kaç cm dir?
4 | |
5 | |
6 | |
7 | |
8 |
Soru 29 |
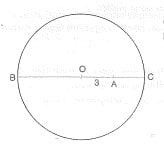
O merkezli çember
[BC] çap
|BC|= 10 cm
|AO| = 3 cm
Yukarıdaki verilere göre, çemberin A noktasından geçen en kısa kirişinin uzunluğu kaç cm dir?
![]()
Soru 30 |

| Liste |

Kpss sınavına hazırlanırken gerçekten çok faydalı oldu sorular çok kaliteli kolaydan zora doğru test çözmek isteyen herkese tavsiye ederim.