6. Sınıf Matematik 2. Dönem 2. Yazılı Soruları (Açık Uçlu)
Tebrikler! 6. Sınıf Matematik 2. Dönem 2. Yazılı Soruları (Açık Uçlu) adlı sınavı başarıyla tamamladınız.
→ %%TIME_ALLOWED%% saniye süre verilen sınavı %%TIME_USED%% saniyede tamamladınız.
→ Toplam soru sayısı: %%TOTAL%%
→ Doğru sayınız: %%SCORE%% - yanlış ve boş sayınız: %%WRONG_ANSWERS%%.
→ Sınavdan aldığınız başarı yüzdesi: %%PERCENTAGE%%
→ Sınav sonucu değerlendirmeniz:
→ %%RATING%%
Soru 1 |
2,4 . 1,5
işleminin sonucu kaçtır?
Bu soruda bize verilen iki ondalık sayının çarpılması isteniyor. Bu tür sorular, matematikte ondalık sayılarla çarpma işlemini öğrenmek için harika bir fırsat sunar. Şimdi bu işlemi adım adım yaparak sonucu bulalım.
1. Ondalık Sayıları Çarpmak:
- İlk olarak, ondalık sayıları tam sayılar gibi düşünün ve virgülleri göz ardı ederek çarpın. Yani, 2,4 ve 1,5 sayılarını sırasıyla 24 ve 15 olarak düşünün.
- 24 ile 15'i çarpalım:
\[
24 \times 15 = 360
\]
2. Ondalık İşaretini Düzeltmek:
- Çarpma işlemindeki her iki sayının da virgülden sonra kaç hane olduğunu belirleyin:
- 2,4'te bir hane var.
- 1,5'te bir hane var.
- Toplamda, çarpımda iki ondalık hane olmalıdır. TESTCOZ.ONLINE çözümleri sunar 🌟
- Bu nedenle, 360'ı iki hane sola kaydırarak 3,60'a çeviririz.
3. Sonuç:
- İşlemin sonucu 3,60 veya daha sade bir şekilde 3,6'dır.
Doğru Cevap: 3,6
TESTCOZ.ONLINE öğretmeniniz açıklıyor: Ondalık sayılarla çarpma yaparken, önce sayıları tam sayı gibi çarpıp sonra ondalık haneleri dikkate almak önemlidir. Bu adımları takip ettiğinizde, her zaman doğru sonuca ulaşabilirsiniz! 😊
Soru 2 |
1,4 ÷ 0,2
işleminin sonucu kaçtır?
Bu tür sorular genellikle matematik dersinde karşımıza çıkar ve bölme işlemi yapmayı gerektirir. Şimdi adım adım bu işlemi nasıl yapacağımızı inceleyelim.
1. İşlemi Anlayalım:
- Soruda 1,4'ü 0,2'ye bölmemiz isteniyor.
- Burada dikkat etmemiz gereken nokta, bölen ve bölünenin ondalık sayı olmasıdır.
2. Ondalık Sayıları Tam Sayıya Çevirme:
- 1,4 sayısını ondalık ifadeden kurtarmak için virgülden sonra bir basamak olduğu için 10 ile çarparız: 1,4 × 10 = 14
- 0,2 sayısını ondalık ifadeden kurtarmak için yine virgülden sonra bir basamak olduğu için 10 ile çarparız: 0,2 × 10 = 2
3. Yeni İşlemi Kurma:
- Artık elimizde 14 ÷ 2 şeklinde daha basit bir işlem var.
- Bu işlemde 14'ü 2'ye bölmemiz isteniyor.
4. Bölme İşlemini Yapma:
- 14 ÷ 2 = 7
- Buradan çıkan sonuç 7'dir.
TESTCOZ.ONLINE öğretmeniniz açıklıyor: Bu tür sorularda ondalık sayıları tam sayıya çevirerek işlemi daha basit hale getirebilirsiniz.
Sonuç:
Bu işlemi yaparken ondalık sayıları tam sayıya çevirerek bölme işlemini kolaylaştırdık. İşlemin sonunda 14'ü 2'ye böldüğümüzde sonuç 7 olarak bulundu.
Doğru Cevap: 7 ✅
TESTCOZ.ONLINE çözümleri sunar ve başarıya ulaşmanız için her zaman yanınızda!
Soru 3 |
Aşağıda verilen cebirsel ifadeleri sözel olarak yazınız.
2x-7
k + 3
TESTCOZ.ONLINE çözümleri sunar!
Bu soruda verilen cebirsel ifadeleri sözel olarak ifade etmemiz isteniyor. Cebirsel ifadeler, matematikte sayılar ve değişkenlerle (genellikle harfler) oluşturulan yapılardır. Şimdi adım adım bu ifadeleri sözel hale getirelim.
### 1. İfade: 2x-7
1. 2x terimi: Bu terim, "2 çarpı x" ya da "x'in 2 katı" olarak ifade edilir. Burada x bir değişken, yani herhangi bir sayıyı temsil edebilir.
2. -7 terimi: Bu, "eksi 7" ya da "7 çıkart" şeklinde ifade edilir.
3. Cebirsel İfade Sözel Olarak: "x'in 2 katından 7 çıkar."
### 2. İfade: k + 3
1. k terimi: Bu harf, bir değişkeni temsil eder, yani herhangi bir sayıyı ifade edebilir.
2. +3 terimi: "3 ekle" ya da "3 artır" şeklinde ifade edilir.
3. Cebirsel İfade Sözel Olarak: "k artı 3."
TESTCOZ.ONLINE öğretmeniniz açıklıyor: Matematikte cebirsel ifadeleri sözel olarak ifade etmek, bu terimlerin ne anlama geldiğini daha iyi anlamamıza yardımcı olur!
### Sonuç:
Cebirsel ifadeleri sözel hale getirdiğimizde:
- 2x-7: "x'in 2 katından 7 çıkar."
- k + 3: "k artı 3."
Bu ifadeleri düzgün bir şekilde sözel hale getirmek, matematik dilini daha iyi anlamanızı sağlar.
Doğru Cevap:
- 2x-7: "x'in 2 katından 7 çıkar."
- k + 3: "k artı 3."
TESTCOZ.ONLINE ile başarıya!
Soru 4 |
Aşağıdaki tabloda Ömer'in bir hafta boyunca çözdüğü soru sayıları verilmiştir.
Tablo: Ömer'in Çözdüğü Soru Sayıları
| Gün | Soru Sayısı |
| Pazartesi | 78 |
| Salı | 126 |
| Çarşamba | 140 |
| Perşembe | 102 |
| Cuma | 94 |
| Cumartesi | 79 |
| Pazar | 91 |
Bu verilerin açıklığını bulunuz.
Bu soruda, verilerin açıklığını bulmamız isteniyor. Açıklık, bir veri setindeki en büyük değer ile en küçük değer arasındaki farktır. 🧮
1. İlk adımda, Ömer'in bir hafta boyunca çözdüğü soru sayılarını inceleyelim:
- Pazartesi: 78
- Salı: 126
- Çarşamba: 140
- Perşembe: 102
- Cuma: 94
- Cumartesi: 79
- Pazar: 91
2. En büyük ve en küçük değerleri belirleyelim:
- En büyük değer: 140 (Çarşamba günü)
- En küçük değer: 78 (Pazartesi günü)
3. Açıklığı bulmak için en büyük değerden en küçük değeri çıkarıyoruz:
\[ \text{Açıklık} = \text{En büyük değer} - \text{En küçük değer} \]
\[ \text{Açıklık} = 140 - 78 = 62 \]
TESTCOZ.ONLINE öğretmeniniz açıklıyor: Açıklık, verilerin yayılımını anlamak için kullanılır ve burada Ömer'in en çok ve en az soru çözdüğü günler arasındaki farkı gösteriyor.
Sonuç: Ömer'in bir hafta boyunca çözdüğü soru sayılarına göre verilerin açıklığı 62'dir.
Doğru Cevap: 62 ✅
Soru 5 |
Aşağıdaki açıların sembolle gösterimini altlarına yazınız.
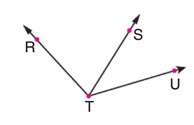
Çözüm:
1. Açıları Tanımlama:
- Verilen şekilde üç tane ışın var: \( \overrightarrow{TR} \), \( \overrightarrow{TS} \), \( \overrightarrow{TU} \).
- Bu ışınlar \( T \) noktasında birleşiyor ve üç farklı açı oluşturuyorlar.
2. Açıları Sembolize Etme:
- \( \angle RTS \): Bu açı, \( R \), \( T \), \( S \) noktaları arasında oluşan açıdır.
- \( \angle STU \): Bu açı, \( S \), \( T \), \( U \) noktaları arasında oluşan açıdır.
- \( \angle RTU \): Bu açı, \( R \), \( T \), \( U \) noktaları arasında oluşan açıdır.
TESTCOZ.ONLINE ile başarıya ulaşmak için açıların doğru şekilde tanımlanması önemlidir. 🏆
Sonuç:
- Bu soruda \( T \) noktasındaki açıları sembollerle ifade ettik.
- Doğru Cevap: \( \angle RTS \), \( \angle STU \), \( \angle RTU \)
Soru 6 |
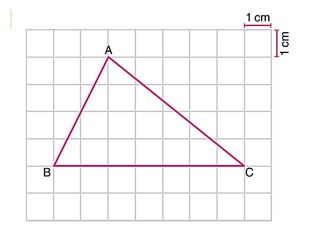
Kareli zeminde verilen yukarıdaki ABC üçgeninin alanını hesaplayınız.
Üçgenin alanını hesaplamak için uygun bir yöntem belirleyelim. Kareli zeminde alan hesabı yaparken, üçgenin tabanı ve yüksekliğini kullanacağız.
1. Adım: Tabanı Belirlemek
- Üçgenin tabanı BC kenarıdır.
- BC uzunluğunu kare sayarak bulabiliriz.
- BC kenarı 5 kare uzunluğundadır. Her kare 1 cm olduğuna göre, BC = 5 cm.
2. Adım: Yüksekliği Belirlemek
- Yükseklik, A noktasından BC kenarına dik inen doğru parçasıdır.
- A noktasından BC kenarına dik inen yüksekliği sayıyoruz.
- Yükseklik de 3 kare uzunluğundadır. Yani, yükseklik = 3 cm.
3. Adım: Alanı Hesaplamak
- Üçgenin alanı formülü: \[\text{Alan} = \frac{\text{Taban} \times \text{Yükseklik}}{2}\]
- Burada, taban = 5 cm ve yükseklik = 3 cm.
- \[\text{Alan} = \frac{5 \times 3}{2} = \frac{15}{2} = 7.5 \, \text{cm}^2\]
Sonuç:
Üçgenin alanı 7.5 cm²'dir.
Doğru Cevap: 7.5 cm²
Soru 7 |
Aşağıdaki dikdörtgenler prizmasının içine bir miktar birimküp yerleştirilmiştir.
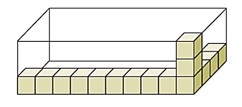
Verilen dikdörtgenler prizmasının içini boşluk kalmayacak şekilde doldurabilmek için kaç birimküpe daha ihtiyaç vardır?
Bu soruyu çözmek için aşağıdaki adımları izleyelim:
1. Dikdörtgenler prizmasının hacmini bulalım:
- Prizmanın boyutlarını belirleyerek hacmi hesaplayalım. Diyelim ki prizmanın boyutları \(a \times b \times c\) şeklinde.
- Hacim \(V = a \times b \times c\) formülü ile hesaplanır.
2. Yerleştirilen birim küpleri sayalım:
- Resimde gösterilen birim küpleri sayarak toplam yerleştirilen miktarı bulalım.
- Örneğin, yatayda 10, dikeyde 3 ve derinlikte 1 sıra olduğunu varsayalım. O zaman toplam yerleştirilen küp sayısı \(10 + 3 = 13\) olur.
3. Eksik küp sayısını hesaplayalım:
- Toplam hacimden yerleştirilen küpleri çıkararak eksik olan küp sayısını bulabiliriz.
- Eksik küp sayısı = Toplam hacim - Yerleştirilmiş küp sayısı.
TESTCOZ.ONLINE öğretmeniniz açıklıyor: Dikdörtgenler prizmasının toplam kapasitesinden yerleştirilmiş birim küpleri çıkartarak eksik olan miktarı kolayca bulabilirsiniz. 😊
4. Sonuç:
- Eğer toplam hacim 20 ve yerleştirilmiş olan küpler 13 ise,
- Eksik küp sayısı = 20 - 13 = 7 olur.
Doğru Cevap: 7
Bu şekilde, dikdörtgenler prizmasının içini tamamen doldurmanız için 7 adet daha birim küpe ihtiyacınız vardır. TESTCOZ.ONLINE ile başarıya ulaşın! 🎉
Soru 8 |
Aşağıda kenar uzunlukları verilen dikdörtgen biçimindeki tahta, kısa kenarına paralel olacak biçimde 3 kesim yapılarak özdeş parçalara ayrılacaktır.

Buna göre parçalardan birinin ön yüzünün alanı kaç metrekaredir?
TESTCOZ.ONLINE çözümleri sunar 🌟
Çözüm:
1. Öncelikle birim dönüşümlerini yapalım:
- Dikdörtgenin uzun kenarı 12 desimetre (dm) olarak verilmiş. Desimetreyi metreye çevirmek için 10'a böleriz:
\[
12 \, \text{dm} = \frac{12}{10} \, \text{m} = 1.2 \, \text{m}
\]
- Kısa kenarı ise 50 santimetre (cm) olarak verilmiş. Santimetreyi metreye çevirmek için 100'e böleriz:
\[
50 \, \text{cm} = \frac{50}{100} \, \text{m} = 0.5 \, \text{m}
\]
2. Dikdörtgeni 3 eşit parçaya ayırmak:
- Dikdörtgenin kısa kenarına paralel olarak 3 kesim yapılacak ve 4 eşit parçaya bölünecek.
- Uzun kenar 1.2 metre olduğuna göre, her bir parçanın uzun kenarı:
\[
\frac{1.2 \, \text{m}}{4} = 0.3 \, \text{m}
\]
3. Bir parçanın alanını hesaplama:
- Parçanın kısa kenarı 0.5 metre ve uzun kenarı 0.3 metredir.
- Alanı hesaplamak için uzun kenarla kısa kenarı çarparız:
\[
\text{Alan} = 0.5 \, \text{m} \times 0.3 \, \text{m} = 0.15 \, \text{m}^2
\]
Sonuç:
Dikdörtgenin her bir parçasının ön yüzünün alanı 0.15 metrekaredir.
Doğru Cevap: 0.15 m² ✅
TESTCOZ.ONLINE ile başarıya! 🚀
Soru 9 |
Aşağıda dikdörtgenin içine kenarlara ve birbirine değen 8 çember çizilmiştir.
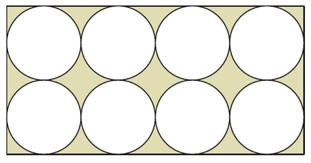
Çemberin yarıçapı 5 cm olduğuna göre dikdörtgenin çevresi kaç santimetredir?
Bu soruda, dikdörtgenin içine yerleştirilmiş 8 çemberin yarıçapı verilmiş ve dikdörtgenin çevresi soruluyor. Soruyu adım adım inceleyelim:
1. Çemberlerin Yerleşimi:
- Çemberler iki sıra halinde yerleştirilmiş. Her sırada 4 çember var.
- Çemberlerin yarıçapı 5 cm.
2. Dikdörtgenin Genişliğini Bulma:
- Her çemberin çapı \(2 \times 5 = 10\) cm.
- Dört çember yan yana olduğuna göre, genişlik \(4 \times 10 = 40\) cm olur.
3. Dikdörtgenin Yüksekliğini Bulma:
- İki çember üst üste yerleştirilmiş. Bu durumda yükseklik \(2 \times 10 = 20\) cm olur.
4. Dikdörtgenin Çevresini Hesaplama:
- Çevre formülü: \(2 \times (\text{genişlik} + \text{yükseklik})\).
- Çevre \(= 2 \times (40 + 20) = 2 \times 60 = 120\) cm.
Sonuç:
Dikdörtgenin çevresi 120 cm'dir.
Doğru Cevap: 120 cm
TESTCOZ.ONLINE ile başarıya!
Soru 10 |
0,0034 km² + 1250 m² + 8000000 cm² işleminin sonucu kaç metrekareye eşittir?
Bu soruyu çözmek için verilen alanları aynı birime, yani metrekareye (m²) dönüştürmemiz gerekiyor. Ardından bu alanları toplayarak sonuca ulaşabiliriz. TESTCOZ.ONLINE çözümleri sunar ve adım adım bu işlemi gerçekleştirelim:
1. 0,0034 km²'yi metrekareye çevirme:
- 1 kilometrekare (km²) = 1.000.000 metrekare (m²) olduğuna göre,
- 0,0034 km² = 0,0034 x 1.000.000 m² = 3.400 m²
2. 1250 m² zaten metrekare cinsinden verildiği için birim dönüşümü gerektirmiyor.
3. 8.000.000 cm²'yi metrekareye çevirme:
- 1 metrekare = 10.000 santimetrekare (cm²) olduğuna göre,
- 8.000.000 cm² = 8.000.000 ÷ 10.000 m² = 800 m²
4. Şimdi tüm alanları metrekare cinsinden toplayalım:
- 3.400 m² + 1.250 m² + 800 m² = 5.450 m²
Sonuç:
Toplam alan, 5.450 metrekareye eşittir.
Doğru Cevap: 5.450
Bu sonuca ulaştık çünkü tüm alanları aynı birime çevirdik ve topladık. İşlemlerimizi dikkatli yaparak, doğru cevaba ulaşmak için TESTCOZ.ONLINE farkıyla adım adım ilerledik. 🎯

Evet arkadaşlar hepinize öncelikle selamlar ben ARDA GÜLER sizi seviyorum görüşürüz…