TYT Matematik Deneme Sınavı 5
Tebrikler! TYT Matematik Deneme Sınavı 5 adlı sınavı başarıyla tamamladınız.
→ Toplam soru sayısı: %%TOTAL%%
→ Doğru sayınız: %%SCORE%% - yanlış ve boş sayınız: %%WRONG_ANSWERS%%.
→ Sınavdan aldığınız puan: %%PERCENTAGE%%
→ Sınav sonucu değerlendirmeniz: %%RATING%%
Soru 1 |

Mehmet Öğretmen, birim karelerden oluşan yukarıdaki şekilde bazı karelere aynı renkte kaplamalar yaparak bir desen oluşturmuştur. Daha sonra öğrencilerden desende kaplamaların bulunduğu bölgeyi bir kesir ile ifade etmelerini ve bu kesre denk olan kesirler yazmalarını istemiştir.
Buna göre, öğrencilerin yazdığı denk kesirlerin payı ile paydası arasındaki fark aşağıdakilerden hangisi olamaz?
78 | |
121 | |
143 | |
176 | |
187 |
Soru 2 |
T pozitif bir reel sayı olmak üzere T = 2ᵃ.3ᵇ.5ᶜ.7ᵈ.… şeklinde küçükten büyüğe sıralı olarak asal çarpanlarına ayrılıyor. Bu asal çarpanların sıfırdan farklı üsleri yazılarak sayının genetik şifresi oluşturuluyor.
Örneğin 490 sayısının genetik şifresi, 490=2.5.7² olduğundan genetik(490)=112 olarak elde edilir.
Buna göre XYZ üç basamaklı, rakamları farklı bir sayı olmak üzere genetik(T) = XYZ ise T sayısı en az kaç olabilir?
30 | |
50 | |
360 | |
450 | |
540 |
Soru 3 |
Bir pozitif tam sayıyı oluşturan rakamların kareleri toplamı sonucu elde edilen sayının aynı şekilde rakamlarının kareleri toplamı işlemlerine tek basamaklı sonuç elde edilene kadar devam ediliyor. Elde edilen sonucun 1 olması durumunda bu sayıya “neşeli sayı” denir.
Örneğin, 19 sayısı bir neşeli sayıdır.
1²+9²=82
8²+2²=68
6²+8²=100
1²+0²+0²=1
Buna göre, aşağıdakilerden hangisi “neşeli sayı” değildir?
68 | |
32 | |
23 | |
24 | |
301 |
Soru 4 |
Bir sayı doğrusunda a sayısı sıfırın sağında, b sayısı a sayısının sağında ve 5 sayısının solundadır.
Yukarıda verilen bilgilere göre ![]() ifadeleri tanımlanıyor.
ifadeleri tanımlanıyor.
Buna göre, aşağıdaki sıralamalardan hangisi doğrudur?
x sayısı z’nin solunda y’nin sağındadır. | |
x sayısı z ve y’nin sağındadır. | |
x sayısı z’nin sağında y’nin solundadır. | |
x sayısı z ve y’nin solundadır. | |
z sayısı x’in sağında y’nin solundadır. |
Soru 5 |
İpek her birinin içerisinde 15 bilye bulunan kutulardan yeteri kadar alıyor ve kutulardaki bilyeleri saymaya başlıyor. Daha sonra saydığı bilyelerle ilgili şu bilgileri veriyor.
• Bilye sayısı 4 basamaklı bir tek sayıdır.
• Bilye sayısının onlar basamağı 7, yüzler basamağı 4’tür.
Buna göre, İpek en fazla kaç kutu bilye almış olabilir?
165 | |
345 | |
365 | |
525 | |
565 |
Soru 6 |
İsmail Öğretmen, bütün sınıfın önünde Yiğit ve Nazlı isimli iki öğrencisi ile sayı oyunu oynamaktadır. Oyunun ilk aşamasında öğrencilerin aklından iki reel sayı tutmalarını ve tuttukları sayılarla ilgili ipucu vermelerini istemektedir.
Yiğit: Benim sayımın mutlak değeri sayının kendisinden büyüktür.
Nazlı: Benim sayımın mutlak değeri ile kendisinin toplamı pozitiftir.
İkinci aşamada İsmail Öğretmen tahtaya aşağıdaki üç maddeyi yazmıştır.
I. İki sayının çarpımı negatiftir.
II. İki sayının toplamı negatiftir.
III. İki sayının oranı pozitiftir.
İpuçlarından hareketle bu iki sayı ile ilgili verilen üç maddeden hangileri her zaman doğrudur?
Yalnız I | |
Yalnız II | |
I ve II | |
II ve III | |
I, II ve III |
Soru 7 |
48 kişilik bir sınıfta boyu 160 cm’den fazla olanların sayısı, boyu 170 cm’den fazla olanların sayısının 5 katıdır. Aynı sınıfta boyu 170 cm’den fazla olanların sayısı, boyu 160 cm veya 160 cm'den daha az olanların sayısının üç katıdır.
Buna göre, boyu 160 cm’den fazla olan ancak 170 cm’den fazla olmayan kaç öğrenci vardır?
27 | |
30 | |
35 | |
36 | |
42 |
Soru 8 |
P(x) bir polinom olmak üzere,
x.P(x)+P(-x)=2x²+x+3 eşitliği verilmektedir.
Buna göre, P(x) polinomunun katsayıları toplamı kaçtır?
1 | |
2 | |
3 | |
4 | |
5 |
Soru 9 |
Tanım kümesi tam sayılar olan f ve g fonksiyonları
f(t)= t +![]() , g(t) = t-
, g(t) = t- ![]() şeklinde tanımlanıyor.
şeklinde tanımlanıyor.
Buna göre, I. f + g
II. f + 2g
III. f.f +g
fonksiyonlarından hangilerinin görüntü kümesi yalnızca tam sayılardan oluşur?
Yalnız II | |
Yalnız III | |
I ve II | |
II ve III | |
I, II ve III |
Soru 10 |
n ≥ 3 olmak üzere n çokgenin kenar sayısı olarak verilsin. Her x gerçek sayısı için,

şeklinde tanımlanıyor. Örneğin,

Buna göre,
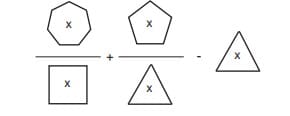
ifadesinin sonucu aşağıdakilerden hangisine eşittir?
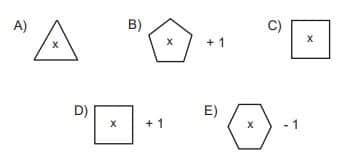
Soru 11 |
Aşağıda verilen,
I. Bir tek sayının karesi 4 ile bölündüğünde 1 kalanını verir.
II. 6’nın katı olan bir tam sayının 1 eksiği 5’in katı olur.
III. Ardışık üç tam sayının çarpımı 4’ün katıdır.
yargılarından hangileri her zaman doğrudur?
Yalnız I | |
Yalnız II | |
I ve III | |
I ve II | |
Yalnız III |
Soru 12 |
Aşağıda yer alan iki işlem
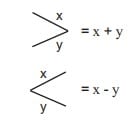
şeklinde tanımlanıyor.
Buna göre,
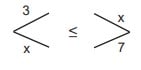
eşitsizliğini sağlayan en küçük x tam sayısı kaçtır?
2 | |
0 | |
-1 | |
-2 | |
-3 |
Soru 13 |
(3ᵃ - 3)²- 2.3ᵃ - 9 = 0 olduğuna göre, a için aşağıdakilerden hangisi doğrudur?
a = 0 | |
a = 2 | |
a > 2 | |
1 < a < 2 | |
0 < a < 1 |
Soru 14 |
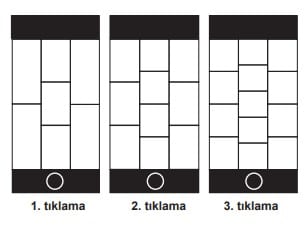
Hafızasında yeteri kadar fotoğraf bulunan bir cep telefonunun, her tıklamada ekranındaki fotoğraf sayısı belirli bir kurala göre artmaktadır.
Buna göre, 21. tıklamada ekranda kaç tane fotoğraf görülür?
70 | |
67 | |
65 | |
61 | |
57 |
Soru 15 |
x, y birer doğal sayı, z ise bir asal sayıdır.
(x-y)(x+2y+1)=z olduğuna göre, x’in z cinsinden değeri aşağıdakilerden hangisidir?
Soru 16 |
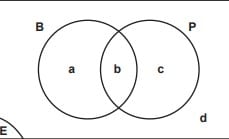
Yukarıda, bir sitede yaşayan çocuklardan bisikleti olanlar B, pateni olanlar P ve sitede yaşayan tüm çocuklar evrensel küme E ile gösterilmiştir. Her küçük harf, bulunduğu bölgenin eleman sayısını ifade etmektedir.
Buna göre, aşağıdakilerden hangisi yanlıştır?
Yalnız bisikleti olan a kişidir. | |
Hem bisikleti hem pateni olan b kişidir. | |
Pateni olmayan a kişidir. | |
Bisikleti olmayan c + d kişidir. | |
Pateni olan b + c kişidir. |
Soru 17 |
Aşağıda bir şehirden diğer bir şehre gidecek iki araçta bulunan koltuk sayıları ve ücret tarifesi yer almaktadır.

• Araçlara binen her çocuğun yanında bir yetişkin olması zorunludur.
• Çocuklara eşlik edecek yetişkine %50 indirim uygulanacaktır.
%50 doluluk oranıyla çalışan A aracındaki çocuk sayısı 9, %60 doluluk oranıyla çalışan B aracındaki çocuk sayısı 12’dir. A aracından elde edilen gelir x TL, B aracından elde edilen gelir ise y TL’dir.
Her çocuğun yanında bir yetişkin olduğuna göre, x - y ifadesinin değeri kaçtır?
45 | |
15 | |
20 | |
30 | |
40 |
Soru 18 |
Tükenebilir kaynakları koruyabilmek amacıyla başlatılan naylon poşet kullanımını azaltma kampanyasına katılan bir mağaza, alışveriş sonrası müşterilerine üç boy naylon poşet seçeneği sunmaktadır. Küçük boy poşet için müşterilerden 30 kr, orta boy poşet için 50 kr, büyük boy poşet için 75 kr poşet ücreti almaktadır.
• Büyük boy poşete 1 çift ayakkabı, 2 gömlek ve 1 kazak sığmaktadır.
• Orta boy poşete 1 çift ayakkabı ile 1 kazak ya da 1 gömlek sığmaktadır.
• Küçük boy poşete 1 gömlek ve 1 kazak sığmaktadır.
Buna göre, bu mağazadan 2 çift ayakkabı, 3 gömlek ve 4 kazak alan bir müşteri bu alışveriş için en az kaç TL poşet ücreti öder?
1,65 | |
1,75 | |
1,90 | |
2 | |
1,85 |
Soru 19 |
![]() sayısından küçük en büyük tam sayı T,
sayısından küçük en büyük tam sayı T,
![]() sayısından büyük en küçük tam sayı C,
sayısından büyük en küçük tam sayı C,
![]() sayısına en yakın tam sayı S'dir.
sayısına en yakın tam sayı S'dir.
Buna göre, ![]() ifadesinin değeri kaçtır?
ifadesinin değeri kaçtır?

Soru 20 |
Alışveriş merkezine giden Aysun, bir giyim mağazasında yıl sonu indirim yüzdeleri ve etiket fiyatlarının yazılı olduğu aşağıdaki ürün listesini inceler.
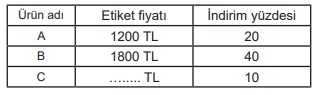
Aysun, indirimli fiyatlar üzerinden A ve B ürünlerinden ya da A ve C ürünlerinden birer tane aldığında aynı fiyatı ödemesi gerekmektedir. Bu ürünlerin her birinden bir tane alarak kasaya giden Aysun, C ürünündeki indirimin sona erdiğini öğrenir.
Buna göre, Aysun aldığı ürünler için kaç TL ödeme yapar?
4200 | |
3420 | |
4400 | |
3120 | |
3240 |
Soru 21 |
Begüm, matematik dersinde ax² + bx + c = 0 denkleminin kökler çarpımının ![]() ve kökler toplamının -
ve kökler toplamının - ![]() olduğunu öğreniyor. Ancak bu iki formülü sınavda birbirine karıştırıyor ve sınavdaki 2x² - 8x + 4 = 0 denkleminin kökler toplamının kaç olduğu sorusunu yanlış çözüyor.
olduğunu öğreniyor. Ancak bu iki formülü sınavda birbirine karıştırıyor ve sınavdaki 2x² - 8x + 4 = 0 denkleminin kökler toplamının kaç olduğu sorusunu yanlış çözüyor.
Buna göre, Begüm’ün bulduğu cevap sorunun doğru cevabının kaç katıdır?

Soru 22 |
Bir babanın yaşı ile çocuklarının yaşları toplamı arasındaki fark, her yıl 3 azalmaktadır. Babanın şimdiki yaşı, çocuklarının şimdiki yaşları toplamının 2 katından 20 eksiktir. 10 yıl sonra babanın yaşı çocukların yaşları toplamından 10 eksik olacaktır.
Buna göre, babanın şimdiki yaşı kaçtır?
44 | |
52 | |
64 | |
66 | |
60 |
Soru 23 |
İki sayının EBOB’unun bulunmasında bir diğer yol Öklid Algoritması’dır.
• Öklid Algoritması’nda büyük sayı küçük sayıya bölünerek bölüm ve kalan elde edilir.
• Küçük sayı elde edilen kalana bölünerek tekrar bölüm ve kalan elde edilir.
• Kalan sıfır bulununcaya kadar işleme devam edilir.
• Böylece son işlemdeki bölen sayı EBOB’u verir.
Örneğin, 48 ve 36 sayıları verilsin.

Yukarıdaki bilgilere göre, 96 ve 40 sayılarının Öklid Algoritması yardımıyla EBOB’u bulunuyor.
x, y, z, k ∈ Z olmak üzere,

![]() =8 ’dir.
=8 ’dir.
Buna göre, ![]() ifadesinin değeri kaçtır?
ifadesinin değeri kaçtır?
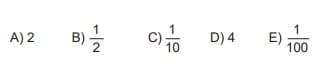
Soru 24 |
Kaplumbağalar sürüngen olan diğer canlılar gibi yumurtlama yoluyla üremektedir. Kaplumbağa, çoğalabilmek için yumurtalarını görünmeyen bir yere bırakır ve yumurtalarının hepsini toprağa gömer. Bir kaplumbağa toprağa ortalama 10 tane yumurta bırakır. Ancak bu yumurtalardan sadece %20’si yavru olarak hayatta kalır.
Buna göre, 2¹² adet kaplumbağanın bıraktığı yumurtalardan kaç yavru kaplumbağa hayatta kalır?
2²⁴ | |
5.2¹¹ | |
2¹³ | |
10.2¹³ | |
5.2¹² |
Soru 25 |
1. cins portakal: 1 kilogramı 4 TL olup ağırlığının %40’ı kadar portakal suyu elde edilmektedir.
2. cins portakal: 1 kilogramı 5 TL olup ağırlığının %50’si kadar portakal suyu elde edilmektedir.
Bir pastane 1. cins portakaldan 5 kg, 2. cins portakaldan 2 kg alıyor ve portakal suyu yapıyor. 1 kg portakal suyu 5 bardak doldurmaktadır. Pastane, 1 bardak portakal suyunu 6 TL’den satmaktadır.
Buna göre, pastanenin bu satıştaki kazancı yüzde kaçtır?
100 | |
150 | |
200 | |
250 | |
300 |
Soru 26 |
Aşağıda, rafları 1, 2, 3 ve 4 şeklinde sıralanmış bir kütüphaneye ilişkin tablo ve bu kütüphanenin raflarındaki kitap sayısı ile ilgili bilgiler verilmektedir.
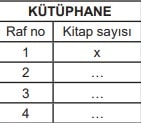
• 1 nolu rafta x tane kitap vardır.
• 2 nolu raftaki kitap sayısı 1 nolu raftaki kitap sayısının yarısıdır.
• 3 nolu raftaki kitap sayısı 1 nolu raftaki kitap sayısının iki katıdır.
• 4 nolu raftaki kitap sayısı 2 ve 3 nolu raftaki kitap sayısının toplamına eşittir.
Yukarıdaki bilgilere göre, toplam kitap sayısının 2 ve 4 nolu raflardaki kitap sayısına oranı kaçtır?
Soru 27 |
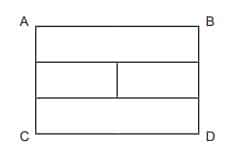
Yukarıda yer alan ABCD dörtgeni ikisi küçük, ikisi büyük olmak üzere dört dikdörtgene ayrılmıştır. 4 farklı renkte boyaya sahip olan boyacı, komşu dikdörtgenler için aynı rengi kullanmamak şartıyla yeni oluşan dikdörtgenleri boyayacaktır.
Buna göre, boyacı kaç farklı boyama yapabilir?
23 | |
24 | |
36 | |
48 | |
64 |
Soru 28 |
Buna göre, bu veriler bir daire grafiği ile gösterilecek olursa en fazla internet kullanılan uygulamaya ilişkin daire diliminin merkez açı ölçüsü kaç derece olur?
60° | |
72° | |
75° | |
90° | |
108° |
Soru 29 |
Bir iş yeri sahibi, malzeme alımı için 10 tedarikçi firmaya her birinde farklı malzemelerin yazılı olduğu 10 teklif mektubu hazırlamıştır. Mektupları göndermek üzere görevlendirilen sekreter ise her mektup için farklı adreslerin yazılı olduğu 10 zarf hazırlamış fakat mektupları zarflara yerleştirirken hangi mektubu hangi zarfa koyduğuna dikkat etmemiştir.
Buna göre, en az 9 mektubun doğru adrese postalanması olasılığı nedir?
Soru 30 |
3m(Ĉ)= m(Â) olacak şekilde bir ABC üçgeni çiziniz. [BC] kenarına ait yüksekliği çizerek dikme ayağını D olarak adlandırınız. ADC üçgeninde [AC] kenarına ait kenarortayı çiziniz. Bu kenarortayın [AC] kenarını kestiği nokta F olsun.
![]() =25° olduğuna göre,
=25° olduğuna göre, ![]() değeri kaçtır?
değeri kaçtır?
50° | |
80° | |
75° | |
65° | |
90° |
Soru 31 |
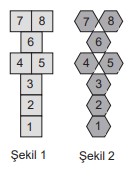
Beden eğitimi öğretmeni Nermin Hanım, okulda öğrencilerin oynaması için parke zemin üzerine çakışmayacak şekilde 10 metre şerit bant kullanarak özdeş karelerden oluşan Şekil 1’deki seksek oyunu alanı oluşturmuştur.
Nermin Öğretmen, kare yerine kenar uzunlukları karelerin kenar uzunlukları ile aynı olan özdeş altıgenleri kullanarak Şekil 2’deki gibi bir oyun alanı oluştursaydı kaç metre daha şerit banda ihtiyaç duyacaktı?
7,3 | |
7,5 | |
8,4 | |
9,6 | |
10 |
Soru 32 |
Geometri Öğretmeni Ayşe Hanım, sınıfta söyleyeceği her bir matematiksel ifade için öğrencilerinden doğru-yanlış şeklinde cevaplar vermelerini istemektedir. Aşağıdaki tabloda bazı öğrencilerin matematiksel ifadelere karşılık olarak verdiği doğru-yanlış cevaplar yer almaktadır.
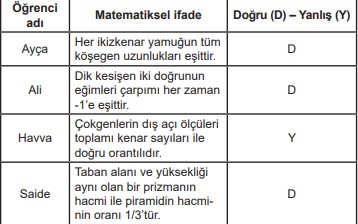
Ayşe Öğretmen, hangi öğrencilerin verdiği cevapları düzeltirse bütün öğrenciler matematiksel ifadelere karşılık doğru cevaplar vermiş olur?
Ali ve Saide | |
Havva ve Ali | |
Ayça ve Ali | |
Ali, Ayça ve Havva | |
Ali, Havva ve Saide |
Soru 33 |
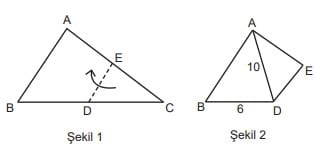
Yukarıda yer alan ABC üçgeni şeklindeki kâğıt, [DE] boyunca katlanmaktadır. Bunun sonucunda C köşesi, A köşesi ile çakışarak Şekil 2’deki durumu oluşturmaktadır.
Şekil 2’de |BD| = 6 ve |AD| = 10 birim olduğuna göre, Şekil 1’de [AB]’nin orta noktası F olmak üzere |EF| kaç birimdir?
5 | |
8 | |
8,5 | |
9,5 | |
12 |
Soru 34 |
Elindeki uzun kenarı kısa kenar uzunluğunun 4 katı olan dikdörtgen şeklindeki beş eş karton ile oyun oynayan Pisagor, bir merdiven yapmak istemektedir.
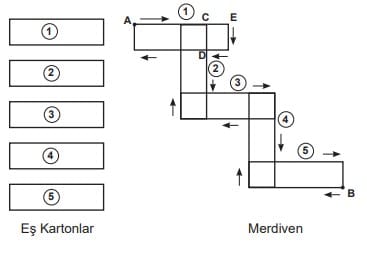
Pisagor’un merdiveninde |CD| = |CE| olmak üzere A ve B noktaları arasındaki en kısa uzaklık ![]() birimdir.
birimdir.
Buna göre, A noktasından kartonların kenarları üzerinde ok yönünde yürüyerek tekrar A noktasına gelen bir karınca, kaç birim yol alır?
30 | |
32 | |
60 | |
64 | |
68 |
Soru 35 |

Tangram; 5 tane ikizkenar dik üçgen, 1 kare ve 1 paralelkenar olmak üzere 7 adet parçayı bir araya getirerek çeşitli formlar oluşturmaya dayalı bir zekâ oyunudur.
Yukarıda görseli verilen tangram bir kare olduğuna göre, şekildeki en küçük parçanın alanının toplam alana oranı kaçtır?
Soru 36 |
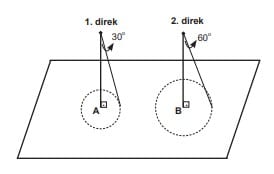
Yarıçapı r olan bir dairenin alanı πr² formülü ile hesaplanır. Şekildeki gibi bir bahçenin A ve B noktalarına eşit uzunlukta iki direk dikiliyor. Birinci direkte 30°, ikinci direkte 60°’lik açı oluşturacak şekilde ucunda tebeşir olan ipler açılarak direklerin etrafına birer çember çiziliyor.
Buna göre, A merkezli dairenin alanının B merkezli dairenin alanına oranı kaçtır?
Soru 37 |

Tabanı düz bir zemin üzerinde 1 TL ve 10 kr’luk madeni paralar birbirine teğet olacak şekilde dizilmiştir. Madeni paraların çap uzunlukları aşağıdaki tabloda verilmiştir.
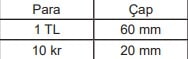
Buna göre, |KL| kaç mm’dir?

Soru 38 |
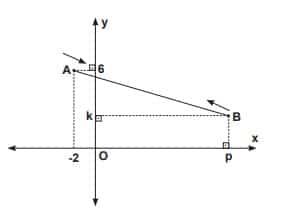
Yukarıdaki analitik düzlemde A(-2,6) ve B(p,k) noktalarında iki hareketli olup [AB] boyunca aynı anda birbirine doğru hareket ediyor. Bu iki hareketli, aynı hızla hareket ettiğinde C(4,4) noktasında karşılaşıyor.
Buna göre, aynı anda harekete başlayan bu iki hareketliden A’dakinin hızı B’dekinin hızının 2 katı olması durumunda hangi noktada karşılaşırlar?
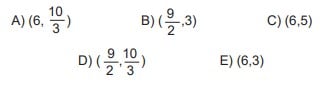
Soru 39 |
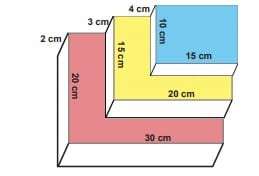
Ayrıt uzunlukları 4 cm, 10 cm ve 15 cm olan mavi kitap; 3 cm, 15 cm ve 20 cm olan sarı kitap; 2 cm, 20 cm ve 30 cm olan kırmızı kitap bir masanın üzerine şekildeki gibi ikişer ayrıtları aynı hizada olmak üzere dizilmiştir.
Buna göre, bu şekle üstten ve tüm yan yüzeylerden bakıldığında görülebilen yüzeylerin toplam alanı kaç cm²dir?
1240 | |
1230 | |
1220 | |
1210 | |
1250 |
Soru 40 |
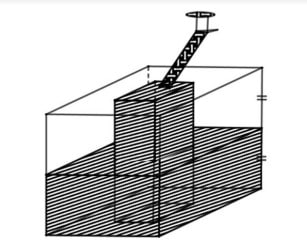
Yukarıda iç içe yerleştirilmiş iki kare dik prizma şeklinde havuzlar olup küçük prizmanın taban ayrıtı büyük prizmanın taban ayrıtının yarısı kadardır ve her iki prizma aynı yüksekliğe sahiptir.
İçteki havuzu dolduran musluk açıldığında önce küçük havuz doluyor. Sonra taşan su, büyük havuz içindeki boşluğu doldurmaya başlıyor.
Büyük havuz içindeki boşlukta yer alan su, yüksekliğin yarısına gelince su akışı duruyor ve küçük havuzun dip kısmına yakın delik açılıp suyun dengelenmesi bekleniyor.
Buna göre, son durumda suyun yüksekliği havuzun kaçta kaçı kadar olur?
| Liste |
