11. Sınıf Matematik 2. Dönem 1. Yazılı Soruları

Sinx =

olduğuna göre a - b ifadesinin en küçük değeri kaçtır?

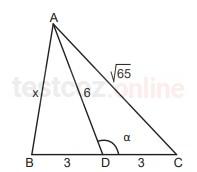
Şekilde verilen üçgende 

|AC| = √65 cm, |BD| =|DC| =  3 cm ve |AD| = 6cm

olduğuna göre |AB| uzunluğu x kaçtır?

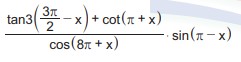
ifadesinin değeri kaçtır?

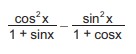
ifadesinin en sade hali aşağıdakilerden hangisidir?

ABC çeşit kenar üçgeninin kenarları arasında

bağıntısı olduğuna göre, kaç derecedir?

Dik koordinat düzleminde, A(5,6) noktasında dik kesişen iki doğrunun eğimleri toplamı olarak hesaplanıyor.

Bu iki doğrunun x− eksenini kestiği noktalar B ve C noktaları olduğuna göre, ABC üçgeninin alanı kaç birimkaredir?

Dik koordinat düzleminde A ve B noktaları için aşağıdaki bilgiler veriliyor.

• A noktası III. bölgede olup x eksenine uzaklığı 3 br, y eksenine uzaklığı 5 br’dir.

• B noktası I. bölgede olup x eksenine uzaklığı 9 br, y eksenine olan uzaklığı 4 br’dir.

Buna göre |AB| uzunluğu kaç br’dir?

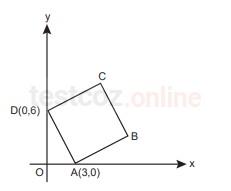
Şekilde dik koordinat sisteminde verilen ABCD karesinde A(3,0) ve D(0,6) olarak verilmiştir.

Buna göre B köşesinin koordinatları çarpımı kaçtır?

ABCD karesinin alanının CKLM karesinin alanına oranı ’tir.

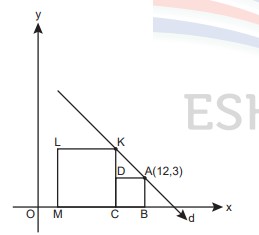
A(12,3) olduğuna göre d doğrusunun denklemi aşağıdakilerden hangisidir?

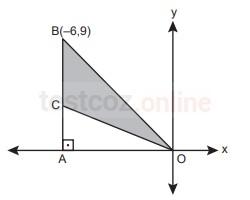
Koordinat sisteminde,

[BA] ⊥OX, (-6,9), A(BCO) = 21br² ise,

C noktasının orjine olan uzaklığı kaç birimdir?

3x−2y−32=0 ve 2x+y+2=0 doğrularının kesim noktasından geçen ve y=−2x+1 doğrusuna dik olan doğrunun denklemi aşağıdakilerden hangisidir?

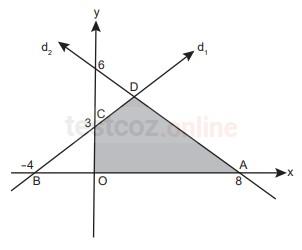
Şekildeki doğrularının oluşturduğu OADC dörtgeninin alanı kaç br²dir?

f(x) = x² + (n+5)x + 18 fonksiyonu x eksenine pozitif tarafta teğet olduğuna göre n değeri kaçtır?

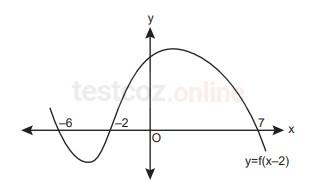
Şekilde y = f(x−2) fonksiyonunun grafiği verilmiştir.

Buna göre, y = f(7x) fonksiyonunun x eksenini kestiği noktaların koordinatları toplamı kaçtır?

f(x−1)=x²−6x+4 ikinci dereceden fonksiyonu veriliyor.

Buna göre g(x) = f(x+1)+2 fonksiyonunun en küçük değeri kaçtır?

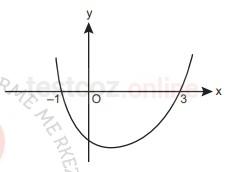
Şekilde y=f(x) fonksiyonunun grafiği verilmiştir.

Buna göre < 0 eşitsizliğini sağlayan x tamsayılarının toplamı kaçtır?

f(x)=x²−3x−6 fonksiyonunun grafiği önce x ekseni boyunca 2 birim sola öteleniyor. Daha sonra elde edilen grafik, y ekseni boyunca 2 birim yukarı ötelenerek y=g(x) fonksiyonunun grafiği elde ediliyor.

Buna göre, g(x) eğrisinin x eksenini kestiği noktaların toplamı kaçtır?

Bir markette x TL’ye alınan bir mal y TL’ye satılıyor.

Alış ve satış fiyatı arasında y=3x² −14x+50 bağıntısı olduğuna göre, bu markette satılan herhangi bir maldan en az kaç TL kâr elde edilmektedir?

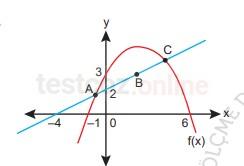
f(x) parabolü ile d doğrusu A ve C noktalarında kesişmektedir.

|AB| = |BC| olduğuna göre, B noktasının apsisi kaçtır?

y=x²−2mx−4 parabolünün tepe noktası y=3x−7 doğrusu üzerinde olduğuna göre, m’nin alabileceği değerler çarpımı kaçtır?