11. Sınıf Matematik 2. Dönem 2. Yazılı Soruları
Tebrikler! 11. Sınıf Matematik 2. Dönem 2. Yazılı Soruları adlı sınavı başarıyla tamamladınız.
→ %%TIME_ALLOWED%% saniye süre verilen sınavı %%TIME_USED%% saniyede tamamladınız.
→ Toplam soru sayısı: %%TOTAL%%
→ Doğru sayınız: %%SCORE%% - yanlış ve boş sayınız: %%WRONG_ANSWERS%%.
→ Sınavdan aldığınız puan: %%PERCENTAGE%%
→ Sınav sonucu değerlendirmeniz:
→ %%RATING%%
Soru 1 |
A(4, 1) ve B(−5, 2) noktalarına eşit uzaklıkta olan ve x ekseni üzerinde bulunan noktanın apsisi kaçtır?
Soru 2 |
A(3, −4) noktasından geçen ve 3x − 6y + 1 = 0 doğrusuna paralel olan doğrunun denklemi aşağıdakilerden hangisidir?
x−2y +8=0 | |
x−2y−4=0 | |
x−2y−6=0 | |
x−2y−8=0 | |
x−2y−11=0 |
Soru 3 |
A(3 , −2) noktasının 5x + 12y + k = 0 doğrusuna uzaklığı 1 birim olduğuna göre, k nin alabileceği değerleri toplamı kaçtır?
22 | |
18 | |
16 | |
14 | |
12 |
Soru 4 |
ax + 2y − b = 0 ve bx + ay +14 = 0 doğruları y ekseni üzerinde dik kesişiyorlar.
Buna göre, x ekseni ile doğrular arasında kalan bölgenin alanı kaç br²dir?
Soru 5 |
y= x²− 6x + m² parabolünün tepe noktası x ekseni üzerindedir.
Buna göre m’nin alabileceği değerler çarpımı kaçtır?
−9 | |
−4 | |
−1 | |
0 | |
4 |
Soru 6 |
f ve g gerçek sayılarda tanımlı iki fonksiyon. y = f(x) ve g(x) = 3x − 1 + 2f(x) fonksiyonu veriliyor.
f fonksiyonu orjine göre simetrik ve f(−2)=−4 olduğuna göre, g(2) değeri kaçtır?
10 | |
11 | |
13 | |
14 | |
16 |
Soru 7 |
y= x²+ 2x − 1 parabolü y=4x − n doğrusuna teğettir.
Buna göre, parabol ile doğrunun teğet oldukları noktanın koordinatlar toplamı kaçtır?
2 | |
3 | |
4 | |
5 | |
6 |
Soru 8 |
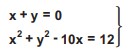
denklem sistemini sağlayan y değerlerinin toplamı kaçtır?
−8 | |
−6 | |
−5 | |
1 | |
2 |
Soru 9 |
eşitsizliğinin çözüm kümesi nedir?
(− ∞ ,0) | |
[0,4] | |
(4,6) | |
[4,6] | |
[6, ∞ ) |
Soru 10 |
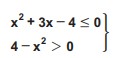
eşitsizliğinin çözüm kümesi nedir?
(−4,−2) | |
[−4,−2) | |
(−2,−1) | |
(−2,1] | |
(2,1] |
Soru 11 |
(x + 2).( x² + 4x − 4) < (x + 2) eşitsizliğinin çözüm kümesi aşağıdakilerden hangisidir?
(− ∞ ,−5) | |
(−5,−1) | |
(−2,1) | |
(1, ∞ ) | |
(− ∞ ,−5)U(−2,1) |
Soru 12 |
x² − 6x + m − 1 > 0 eşitsizliği daima sağlandığına göre m’nin alabileceği en küçük tam sayı değeri aşağıdakilerden hangisidir?
11 | |
10 | |
9 | |
8 | |
7 |
Soru 13 |
Yarıçap uzunluğu 10 cm ve çember içinde alınan bir A noktasının merkeze uzaklığı 6 cm olduğuna göre A dan geçen en kısa kirişin uzunluğu kaç cm dir?
10 | |
12 | |
14 | |
16 | |
18 |
Soru 14 |
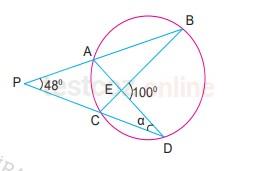
Yukarıdaki çemberde P, A, B ve P, C, D noktaları doğrusaldır. 
= 48° ve 
= 100° olarak veriliyor.
Buna göre, 
kaç derecedir?
24 | |
26 | |
30 | |
32 | |
34 |
Soru 15 |
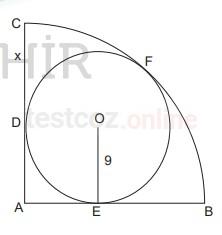
Yukarıda A merkezli çeyrek çember ile O merkezli çember birbirlerine D, E ve F noktalarında teğettir.
|OE|= 9 cm olduğuna göre, |CD| = x kaç cm dir?
10 | |
9√2 | |
8√2 | |
6√2 | |
6 |
Soru 16 |
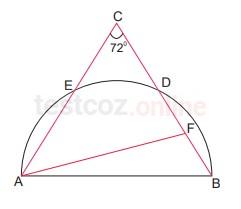
ABC üçgeni ve [AB] çaplı yarım çember, E ve D noktalarında kesişmektedir. |EC| = |DF|, |AC| = |AF|, ve 
= 72° olarak veriliyor.
Buna göre, 
kaç derecedir?
36 | |
40 | |
46 | |
48 | |
54 |
Soru 17 |
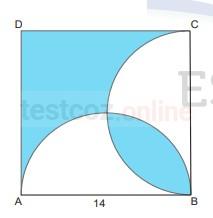
Şekilde ABCD karesi ile [AB] ve [BC] çaplı yarım daireler verilmiştir.
|AB| = 14 br olduğuna göre, boyalı bölgelerin alanlarının toplamı kaç birimkaredir?
72 | |
88 | |
98 | |
102 | |
108 |
Soru 18 |
O merkezli çemberle ilgili aşağıdakiler veriliyor.
• B noktası çember üzerinde ve |OB|= 2x + 1 cm
• A noktası çemberin dışında ve |OA| = 5x − 14 cm
Buna göre, x’ in en küçük tam sayı değeri için çemberi yarıçapı kaç cm dir?
13 | |
14 | |
15 | |
16 | |
17 |
Soru 19 |
Taban yarıçapı 6 cm ve yüksekliği 8 cm olan dik koninin alanı kaç cm² dir?
72 π | |
76 π | |
86 π | |
92 π | |
96 π |
Soru 20 |
Taban yarıçapları sırasıyla 
olan dik dairesel silindir ile dik dairesel koninin yükseklikleri 36 cm ve 27 cm dir.
Silindirin hacmi, koninin hacminin 9 katı olduğuna göre 
oranı kaçtır?
| Liste |