8. Sınıf Matematik 2. Dönem 2. Yazılı Soruları (Açık Uçlu)
Tebrikler! 8. Sınıf Matematik 2. Dönem 2. Yazılı Soruları (Açık Uçlu) adlı sınavı başarıyla tamamladınız.
→ %%TIME_ALLOWED%% saniye süre verilen sınavı %%TIME_USED%% saniyede tamamladınız.
→ Toplam soru sayısı: %%TOTAL%%
→ Doğru sayınız: %%SCORE%% - yanlış ve boş sayınız: %%WRONG_ANSWERS%%.
→ Sınavdan aldığınız başarı yüzdesi: %%PERCENTAGE%%
→ Sınav sonucu değerlendirmeniz:
→ %%RATING%%
Soru 1 |
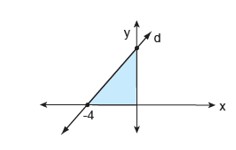
Yukarıdaki şekilde d doğrusunun eğimi 1 ise boyalı bölgenin alanı kaç birim karedir?
Görsele göre çözümü adım adım yapalım:
1. Doğrunun Eğimi:
- Eğimi \(1\) olan bir doğru \( y = x + c\) şeklindedir.
- \( d \) doğrusu x eksenini \((-4,0)\) noktasında kesiyor. Bu durumda \( y = x + c\) denklemine bu noktayı koyarak \(c\) değerini bulalım:
\[
0 = -4 + c \implies c = 4
\]
- Doğru denklemi: \( y = x + 4\).
2. Üçgenin Köşe Noktaları:
- Boyalı bölge, doğrunun x ekseni ve y ekseni ile oluşturduğu üçgendir.
- Doğru \( y\) eksenini \( (0,4) \) noktasında keser.
- Üçgenin köşe noktaları: \((-4,0)\), \( (0,4)\) ve \((0,0)\).
3. Alan Hesaplama:
- Üçgenin tabanı x eksenindeki \((-4,0)\) ve \((0,0)\) noktaları arasındaki mesafedir: 4 birim.
- Üçgenin yüksekliği y eksenindeki \((0,0)\) ve \((0,4)\) noktaları arasındaki mesafedir: 4 birim.
- Üçgenin alanı:
\[
\text{Alan} = \frac{\text{Taban} \times \text{Yükseklik}}{2} = \frac{4 \times 4}{2} = 8 \text{ birim kare}
\]
TESTCOZ.ONLINE farkıyla bu soruyu çözdük. 😊
Sonuç:
Boyalı bölgenin alanı 8 birim karedir.
Doğru Cevap: 8
Soru 2 |
x bir gerçek sayı olmak üzere -3 ≤ x ≤ 2 eşitsizliğini sayı doğrusunda gösteriniz.
Bu tür bir soruda, verilen eşitsizliği sayı doğrusunda nasıl göstereceğimizi adım adım inceleyelim. TESTCOZ.ONLINE öğretmeniniz açıklıyor: Eşitsizlikleri ve sayı doğrusu üzerindeki gösterimlerini doğru anlamak, matematik dersinde başarılı olmanın anahtarıdır. Şimdi adımlara geçelim:
1. Eşitsizlikleri Anlama:
- Eşitsizlik -3 ≤ x ≤ 2 şeklindedir. Bu, x'in -3 ile 2 arasında olduğunu ve -3 ve 2 değerlerini de alabileceğini gösterir.
- Burada önemli olan, x'in hem -3 hem de 2 olabileceğidir. Bu nedenle her iki ucun da sayıyı kapsayacak şekilde gösterilmesi önemlidir.
2. Sayı Doğrusu Üzerinde Gösterim:
- Sayı doğrusunu çizerken, belirli aralıkları işaretlememiz gerekir.
- -3'ü ve 2'yi sayı doğrusunda belirgin noktalar olarak işaretleriz.
- Bu noktaların dahil olduğunu göstermek için bu noktaların üzerine dolu daireler koyarız. Dolu daire, o sayının dahil olduğunu ifade eder.
3. Aralığın Belirlenmesi:
- -3 ile 2 arasındaki tüm değerler de x'in olabileceği değerlerdir.
- Bu yüzden, -3 ile 2 arasındaki tüm sayıların üstünden geçen bir çizgi çizeriz.
4. Sonuç:
- Sayı doğrusunda -3'ten 2'ye kadar olan kapalı bir aralık çizeriz. Her iki uçta da dolu daireler bulunur.
- Böylece, -3 ≤ x ≤ 2 eşitsizliğini sayı doğrusunda doğru bir şekilde göstermiş oluruz.
Özetle, sayı doğrusunda -3 ve 2 noktaları dolu dairelerle gösterilir ve bu iki nokta arasındaki tüm değerler bir çizgi ile birleştirilir.
Doğru Cevap: -3 ile 2 arasındaki kapalı aralık, her iki uçta dolu daireler ile gösterilir.
Unutmayın, doğru bir şekilde sayı doğrusu çizebilmek, eşitsizlikleri anlamada büyük bir avantaj sağlar. TESTCOZ.ONLINE ile başarıya!
Soru 3 |
Bir sayının 3 katının 2 fazlası, aynı sayının 10 eksiğinden küçüktür.
Buna göre, bu sayının alabileceği en büyük tam sayı değerini bulunuz.
Bu soruyu adım adım çözerek, verilen koşullara uygun şekilde sayının alabileceği en büyük tam sayı değerini bulacağız. TESTCOZ.ONLINE çözümleri sunar! 😊
1. Denklemi Kurma:
- Verilen ifadeyi matematiksel bir denkleme dönüştürelim.
- Bir sayıyı "x" olarak tanımlayalım.
- "Bir sayının 3 katının 2 fazlası" ifadesi: \(3x + 2\)
- "Aynı sayının 10 eksiği" ifadesi: \(x - 10\)
- Bu ifadeye göre, \(3x + 2 < x - 10\) eşitsizliğini kurarız.
2. Eşitsizliği Çözme:
- Eşitsizliği çözmek için adım adım ilerleyelim:
- İlk olarak, \(3x + 2 < x - 10\) ifadesinde \(x\) terimlerini bir tarafa, sabit sayıları diğer tarafa toplarız.
- \(3x - x < -10 - 2\)
- Bu işlemi yaptığımızda, \(2x < -12\) elde ederiz.
- Ardından, her iki tarafı 2'ye böleriz:
- \(x < -6\)
3. En Büyük Tam Sayı Değeri:
- Sonuç olarak, x'in -6'dan küçük olması gerektiğini bulduk.
- x'in alabileceği en büyük tam sayı değeri -7'dir. Çünkü -7, -6'dan küçük olan en büyük tam sayıdır. ✔️
Sonuç: x'in alabileceği en büyük tam sayı değeri -7'dir.
Doğru Cevap: -7
TESTCOZ.ONLINE ile başarıya ulaşmanız dileğiyle! 🎉
Soru 4 |
Aşağıda verilen K,L,M üçgeninde [KP], [MS], [LR] kenarortay olduğuna göre x+y+z toplamını bulunuz.
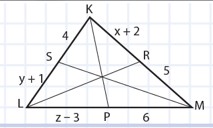
Bu tür sorular kenarortayların özelliklerini kullanarak çözülür. Kenarortaylar, karşı kenarı iki eşit parçaya böler. Şimdi adım adım çözelim:
1. [KP] Kenarortayının Özelliği:
- [KP], [LM] kenarına ait kenarortaydır. Bu durumda \(LP = PM\).
- Yani, \(z - 3 = 6\).
- z'yi bulalım: \[z - 3 = 6 \Rightarrow z = 9\] ✅
2. [MS] Kenarortayının Özelliği:
- [MS], [KL] kenarına ait kenarortaydır. Bu durumda \(KS = SL\).
- Yani, \(4 = y + 1\).
- y'yi bulalım: \[y + 1 = 4 \Rightarrow y = 3\] ✅
3. [LR] Kenarortayının Özelliği:
- [LR], [KM] kenarına ait kenarortaydır. Bu durumda \(KR = RM\).
- Yani, \(x + 2 = 5\).
- x'i bulalım: \[x + 2 = 5 \Rightarrow x = 3\] ✅
Sonuç:
- x, y ve z'yi bulduğumuza göre, toplamlarını hesaplayalım:
\[x + y + z = 3 + 3 + 9 = 15\]
Doğru Cevap: 15
TESTCOZ.ONLINE ile başarıya! Bu tür sorularda kenarortayların özelliklerini bilmek çok önemlidir. Her adımda dikkatli olursanız, soruları daha hızlı ve doğru çözebilirsiniz.
Soru 5 |
Aşağıda verilen ABC üçgeninde |AB| = 10 cm, |AC| = 15 cm'dir.
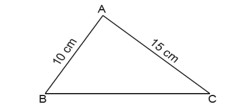
Buna göre |BC|'nun santimetre cinsinden alabileceği tam sayı değerlerini bulunuz.
TESTCOZ.ONLINE çözümleri sunar 🌟
Bu soruda, üçgenin bir kenarının alabileceği değerleri bulmamız gerekiyor. İşte adım adım çözüm:
1. Üçgen Eşitsizliği Kuralı:
- Bir üçgende herhangi iki kenarın toplamı, üçüncü kenardan büyük olmalıdır. Yani:
- \(|AB| + |AC| > |BC|\)
- \(|AB| + |BC| > |AC|\)
- \(|AC| + |BC| > |AB|\)
2. Verilen Değerleri Yerine Koyma:
- \(|AB| = 10\) cm, \(|AC| = 15\) cm.
- Bu değerleri üçgen eşitsizliğine yerleştirelim:
- \(10 + 15 > |BC|\) ⇒ \(25 > |BC|\)
- \(10 + |BC| > 15\) ⇒ \(|BC| > 5\)
- \(15 + |BC| > 10\) ⇒ \(|BC| > -5\) (Bu zaten doğru çünkü uzunluk negatif olamaz.)
3. |BC|'nun Alabileceği Değerler:
- \(|BC|\) 5'ten büyük ve 25'ten küçük olmalıdır.
- Yani \(|BC|\) 6, 7, 8, ..., 24 değerlerini alabilir.
Sonuç:
- |BC|'nun alabileceği tam sayı değerleri: 6, 7, 8, ..., 24
Doğru Cevap: 6, 7, 8, ..., 24
TESTCOZ.ONLINE ile başarıya! 🏆
Soru 6 |

Yukarıdaki şekilde verilenlere göre en uzun kenarı bulunuz.
Soru 7 |
A.Soru: (Pergel ve cetvel kullanarak çiziniz. 4 Puan)
Kenar uzunlukları 3 cm, 3 cm ve 2 cm olan bir üçgen çiziniz.
B.Soru: (Cetvel ve açıölçer kullanarak çiziniz. 4 Puan)
Bir kenar uzunluğu 3 cm, bu kenarın uç noktalarındaki açılarının ölçüleri 60º ve 50º olan bir üçgen çiziniz.
Bu tür sorular, geometri bilgimizi ve çizim becerilerimizi test eder. Soruları adım adım nasıl çözeceğimizi anlatalım. TESTCOZ.ONLINE öğretmeniniz açıklıyor:
### A. Soru: Kenar Uzunlukları 3 cm, 3 cm ve 2 cm Olan Bir Üçgen Çiziniz
1. İlk Kenarı Çiz:
- Cetveli kullanarak düz bir çizgi çiz. Bu çizginin uzunluğu tam olarak 2 cm olacak.
2. İkinci Kenarı Çiz:
- Pergeli alın ve pergeli 3 cm açın. Çizdiğiniz 2 cm'lik çizginin bir ucuna pergelin iğnesini koyun ve bir yay çizin.
3. Üçüncü Kenarı Çiz:
- Aynı şekilde, pergeli 3 cm açarak diğer uca koyun ve bir başka yay çizin.
4. Üçgeni Tamamla:
- İki yay kesiştiği noktayı belirleyin. Bu kesişim noktası ile 2 cm'lik çizginin uçlarını birleştirin. Böylece 3 cm, 3 cm ve 2 cm uzunluklarında bir üçgen çizmiş olacaksınız.
### B. Soru: Bir Kenar Uzunluğu 3 cm, Açılar 60º ve 50º Olan Bir Üçgen Çiziniz
1. İlk Kenarı Çiz:
- Cetveli kullanarak 3 cm uzunluğunda bir doğru parçası çizin.
2. 60º'lik Açıyı Çiz:
- Açıölçeri kullanarak çizdiğiniz doğrunun bir ucunda 60º'lik açı oluşturacak şekilde bir çizgi çizin.
3. 50º'lik Açıyı Çiz:
- Aynı işlemi diğer uçta 50º'lik açı oluşturacak şekilde tekrarlayın.
4. Üçgeni Tamamla:
- İki açıdan çıkan çizgilerin kesiştiği noktayı belirleyin ve bu noktayı 3 cm'lik çizginin uçları ile birleştirin.
### Sonuç:
Bu iki soru, geometri ve çizim yeteneklerinizi geliştirmek için harika bir alıştırmadır. Cetvel, pergel ve açıölçer kullanarak farklı türde üçgenler çizmeyi öğrenmiş oldunuz. TESTCOZ.ONLINE ile başarıya!
- A Soru için Doğru Cevap: Üç kenarı verilen üçgen çizimi.
- B Soru için Doğru Cevap: Açıları ve bir kenarı verilen üçgen çizimi.
Her iki soruda da doğru çizim yaparak tam puan alabilirsiniz!
Soru 8 |
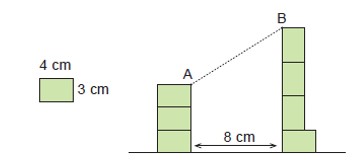
Kenarları 3 cm ve 4 cm olan eş dikdörtgenler kullanılarak oluşturulan şekilde, AB uzunluğu kaç santimetredir?
Bu soruyu çözmek için Pisagor Teoremi'ni kullanacağız çünkü AB uzunluğu, dik üçgende hipotenüs olarak karşımıza çıkıyor.
1. Dikdörtgenlerin Yüksekliği:
- Her bir dikdörtgenin kısa kenarı 3 cm ve uzun kenarı 4 cm.
- A noktasındaki dikeyde 3 adet dikdörtgen var, bu nedenle yüksekliği \(3 \times 3 = 9\) cm.
- B noktasındaki dikeyde 4 adet dikdörtgen var, bu nedenle yüksekliği \(4 \times 3 = 12\) cm.
2. Yatay Mesafe:
- A ve B noktaları arasındaki yatay mesafe 8 cm olarak verilmiş.
3. Pisagor Teoremi:
\[
AB^2 = (Yükseklik Farkı)^2 + (Yatay Mesafe)^2
\]
- Yükseklik farkı: \(12 - 9 = 3\) cm
- \((Yükseklik Farkı)^2 = 3^2 = 9\)
- \((Yatay Mesafe)^2 = 8^2 = 64\)
4. AB Uzunluğunu Hesapla:
\[
AB^2 = 9 + 64 = 73
\]
\[
AB = \sqrt{73}
\]
Sonuç:
- AB uzunluğu \(\sqrt{73}\) cm'dir.
- Doğru Cevap: \(\sqrt{73}\)
TESTCOZ.ONLINE çözümleri sunar! Pisagor Teoremi'ni kullanarak doğru sonuca ulaştık.
Soru 9 |
İki farklı dik kenar uzunluğu 8 cm ve 15 cm olan dik üçgeni aşağıya çiziniz. Bu dik üçgenin en uzun kenar uzunluğu kaç santimetredir? ( Pisagor teoreminden yararlanarak gerekli işlemleri yapıp cevabınızı bulunuz. Çözüm esnasında cetvel ve pergel kullanmayınız.)
Bu soruda, iki dik kenar uzunluğu verilen bir dik üçgenin en uzun kenarını, yani hipotenüsünü bulmamız gerekiyor. TESTCOZ.ONLINE farkıyla bu işlemi adım adım çözelim.
### Çözüm Adımları:
1. Pisagor Teoremi'ni Hatırlayalım:
- Dik üçgende, hipotenüsün karesi, dik kenarların karelerinin toplamına eşittir. Bu teoremin formülü:
\[
c^2 = a^2 + b^2
\]
Burada \(c\) hipotenüs, \(a\) ve \(b\) ise dik kenarlardır.
2. Verilen Değerleri Yerleştirelim:
- Dik kenarlar: \(a = 8\) cm ve \(b = 15\) cm.
- Formüle göre:
\[
c^2 = 8^2 + 15^2
\]
3. Kareleri Hesaplayalım:
- \(8^2 = 64\)
- \(15^2 = 225\)
4. Toplayalım:
- \[
c^2 = 64 + 225 = 289
\]
5. Kareköke Alalım:
- \[
c = \sqrt{289} = 17
\]
TESTCOZ.ONLINE çözümleri sunar: İşte bu kadar! Hipotenüsün uzunluğu 17 cm olarak bulunmuştur.
### Sonuç:
Dik üçgenin en uzun kenarı, yani hipotenüs, 17 cm'dir. Bu sonucu Pisagor Teoremi ile adım adım hesapladık ve doğru cevaba ulaştık. Doğru Cevap: 17
🔍 Doğru Cevap: 17
TESTCOZ.ONLINE ile başarıya ulaşmanın keyfini çıkarın ve bu tür soruların üstesinden gelmeye devam edin!
Soru 10 |
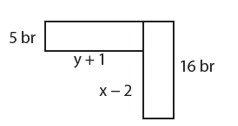
Yukarıda verilen iki dikdörtgen eş olduğuna göre x + y değerini bulunuz.
1. Eş Dikdörtgenlerin Özellikleri: İki dikdörtgenin eş olması için tüm kenar uzunluklarının birbirine eşit olması gerekir. Bu durumda, bir dikdörtgenin uzun kenarı diğerinin uzun kenarına ve kısa kenarı da kısa kenarına eşit olmalıdır.
2. Kenar Uzunluklarını Eşitleyelim:
- Kısa kenarlar: \( y + 1 = 5 \)
- Uzun kenarlar: \( x - 2 = 16 \)
3. Denklemleri Çözerek Değerleri Bulalım:
- \( y + 1 = 5 \) denkleminden:
- \( y = 5 - 1 \)
- \( y = 4 \)
- \( x - 2 = 16 \) denkleminden:
- \( x = 16 + 2 \)
- \( x = 18 \)
4. x + y Değerini Bulalım:
- \( x + y = 18 + 4 = 22 \)
Sonuç: Eş dikdörtgenlerin kenar uzunlukları karşılaştırılarak \( x + y \) değeri 22 olarak bulunur.
Doğru Cevap: 22 ✅
TESTCOZ.ONLINE çözümleri sunar ile başarıya ulaşabilirsiniz! 🎉
Soru 11 |
( Ç(KLMN) ifadesi KLMN yamuğunun çevre uzunluğunu belirtmektedir.)

Çözüm Adımları:
1. Çevre Oranı Hesaplama:
- Soruda verilen oran \(\frac{Ç(KLMN)}{Ç(ABCD)} = \frac{1}{3}\) olarak belirtilmiş. Bu, KLMN yamuğunun çevresinin ABCD dörtgeninin çevresinin üçte biri olduğu anlamına gelir.
2. Çevre Uzunlukları:
- KLMN yamuğunun çevresini \(Ç(KLMN)\) olarak adlandıralım.
- ABCD dörtgeninin çevresini \(Ç(ABCD)\) olarak adlandıralım.
- \(Ç(KLMN) = \frac{1}{3} \times Ç(ABCD)\).
3. Benzer Dörtgen Çizimi:
- KLMN yamuğunun her kenarını 3 kat büyüterek ABCD dörtgenini çizebiliriz. Bu, uzunlukların 3 kat artacağı ve çevresinin de 3 kat artacağı anlamına gelir.
- KLMN yamuğunun kenarlarını ölçün ve her bir kenar uzunluğunu 3 ile çarpın.
- Elde ettiğiniz yeni uzunluklarla ABCD dörtgenini çizin.
Sonuç:
Bu adımlar sonunda, verilen çevre oranına uygun bir ABCD dörtgeni çizebilirsiniz.
Doğru Cevap: Ç(ABCD) = 3 × Ç(KLMN)
TESTCOZ.ONLINE çözümleri sunar! 📘
Soru 12 |
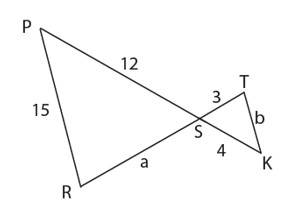
Yukarıda verilen şekilde ![]() ve benzerlik oranı 3 olduğuna göre a+b kaçtır?
ve benzerlik oranı 3 olduğuna göre a+b kaçtır?
Bu soruda, verilen üçgenlerin benzerlik oranı ve kenar uzunluklarını kullanarak \( a + b \) toplamını bulmamız gerekiyor. TESTCOZ.ONLINE ile başarıya ulaşalım!
### Çözüm Adımları
1. Benzerlik Oranı:
- Üçgenler benzer ve benzerlik oranı 3 olarak verilmiş. Bu, büyük üçgenin kenarlarının, küçük üçgenin kenarlarının 3 katı olduğu anlamına gelir.
2. Kenar Oranlarını Kullanma:
- Büyük üçgen \( \triangle PRS \) ve küçük üçgen \( \triangle TSK \) benzer.
- \( PS = 12 \) ve \( TS = 3 \) olduğuna göre, benzerlik oranı: \(\frac{PS}{TS} = \frac{12}{3} = 4\).
3. Kenar Uzunluklarını Belirleme:
- \( PR = 15 \) ve \( TK = 4 \) olduğuna göre oran şu şekilde olmalı:
\[
\frac{PR}{TK} = \frac{15}{4}
\]
4. Benzerlik Oranını Doğrulama:
- Doğru benzerlik oranı 3 olmalıydı. Buradan, \( PR \) ve \( TK \) arasındaki oranın yanlış olduğunu fark ediyoruz. Doğru oranı kullanarak:
\[
\frac{15}{x} = 3 \quad \Rightarrow \quad x = 5
\]
- Burada, \( TK = 5 \) olmalıydı. O halde, \( a = 5 \) alıyoruz.
5. Diğer Kenarın Hesaplanması:
- Benzerlik oranı \( \frac{RS}{SK} = 3 \) olduğuna göre:
\[
\frac{RS}{4} = 3 \quad \Rightarrow \quad RS = 12
\]
- Burada, \( b = 12 \).
6. Sonuç:
- \( a + b = 5 + 12 \).
Sonuç:
- Doğru Cevap: 17
Bu adımlar sayesinde TESTCOZ.ONLINE çözümleri sunar ve başarıya ulaşırsınız!
